Forum de Mathématiques: Maths-Forum

et bien oui dans [0, Pi/4] je trouve 3x ; dans [Pi/4,Pi/2] je trouve -x + Pi et dans [Pi/2,3Pi/4] 2Pi-3x . . .

Bonjour , je dois simplifier la fonction arcsin(sinx)+ arcsin(sin2x) mais voilà j'ai reussi sur les intervalles qui vont de [0,3Pi/4] mais je n'y arrive pas pour le dernier qui est [3Pi/4,Pi].
Merci d'avance.

Bonjour, merci d'avance. Voila mon problème, il faut que je transforme ; sin(3arctanx) Je vous montre mes calculs pour que vous puissiez comprendre plus facilement là où je bloque. sin(3arctanx) = sin(2arctanx+arctanx) = sin(2arctanx)cos(arctanx)+ cos(2arctanx)sin(arctanx) = 2sin(arctanx)cos²(arctan...

Salut, je n'ai pas d'un haut niveau mais je pense que j = e^(2ipi/3)

Veuillez excuser mon retard, je tiens a vous remercier Ericovitchi ainsi qu'aux autres m'ayant consacrer du temps ; j'ai reussi grace a votre precieuse aide a terminer cet exercice . :happy2:
A Bientot.

* = 1-nx ? quand k=0.

Veuillez m'excuser mais je n'arrive pas à trouver le signe ; la formule du binome de Newton me complique les calculs car je me retrouve avec du "

hum effectivement, j'ai pas l'impression que je vais faire des ravages en mathématiques :triste: . Merci beaucoup.

Mais le binome de Newton ce n'est pas qu'avec ?

Salut, quelqu'un pourrait il me dire quel est le truc a voir ou a savoir afin de demontrer cette inégalité ?
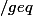1-nx.
Merci.

Non il n'y a pas d'exercice de probabilité proprement dit mais ceci ensuite ; calculer :
*

Une étape, veuillez excuser mon retard.

Ah oui comme cela ça marche, donc ce n'est qu'une erreur d'ennoncé. :hum:
Je vous remercie du temps que vous m'avez consacré.

Salut, oui je viens de vérifier la formule est bien bonne.
Dans l'ennoncé il est precisé que p est plus petit ou egal à n.

Bonjour et merci d'avance. Voilà mon probleme , je dois montrer que ; \begin{pmatrix} n & \\ k & \end{matrix} * \begin{pmatrix} n-k & \\ p-k & \end{matrix} = \begin{pmatrix} p & \\ n & \end{matrix} * \begin{pmatrix} p & \\ k & \end{matrix} J'ai commencer à transformer...

Oh mais oui je suis completement . . . Merci a toi Egan.

Bonjour, je suis novice sur ce forum et je salue tout le monde.. Voila mon probleme ; comment montrer que 2 exposant n est egale à la somme des k allant de 0 à n des k parmis n . Je pense devoir passer par la loi de Bernouilli qui me permettrait de trouver un resultat avec des 1 exposant n mais je n...