22 résultats trouvés
Revenir à la recherche avancée
Bonjour, J'aurais besoin que l'on m'aide à comprendre (plus de détail) l'utilisation du théorème de Stokes ici : On a la fonction F(z)=\mathbb{E}(\frac{zP'_n(z)}{P_n(z)}) oú \mathbb{E} représente l'espérance et P_n(z) et polynôme de degré n. Par le théorèm...
- par MaximusvcUcl
- 07 Aoû 2022, 18:31
-
- Forum: ✯✎ Supérieur
- Sujet: Théorème de Stokes
- Réponses: 1
- Vues: 203
Bonjour, Voici l'énoncé en question (il s'agît d'une introduction heuristique expliquant pourquoi les racines complexes d'un polynôme aléatoire se concentrent autour du cercle unité lorsque n tend vers l'infini) : Supposons que p(z)=a_{0}+...+a_{n}z^{n} est un polynôme à coefficients complex...
- par MaximusvcUcl
- 29 Avr 2022, 14:53
-
- Forum: ✯✎ Supérieur
- Sujet: racines des polynômes aléatoires
- Réponses: 3
- Vues: 332
Bonjour, Voici l'énoncé avec lequel j'ai du mal: Supposons que p(z)=a_{0}+...+a_{n}z^{n} est un polynôme à coefficients complexes aléatoires (iid). Supposons maintenant que \gamma est un cercle plus grand que le cercle unité. Alors \oint_{\gamma}\frac{p'(z)}{p(z)}dz=\oint...
- par MaximusvcUcl
- 29 Avr 2022, 14:29
-
- Forum: ✯✎ Supérieur
- Sujet: racines des polynômes aléatoires
- Réponses: 3
- Vues: 332
Bonjour à tous, Dans le cadre d'un gros projet j'ai besoin d'expliquer une démonstration du mathématicien Edelman. Voici ce qu'il note : On définit \rho_n(x)=\frac{1}{n\pi}\sqrt{\frac{n^4}{x^2(2n+x)^2}-\frac{(n+1)^2(1+x/n)^2n}{((1+x/n)^{2n+2}-1)^2}} . ...
- par MaximusvcUcl
- 18 Avr 2022, 12:40
-
- Forum: ✯✎ Supérieur
- Sujet: (1+x/n)^n
- Réponses: 1
- Vues: 150
Bonjour à tous, Voici l'enoncé : Soit D \subset \textbf{R}^{1+N} un ouvert (la dimension un peu particulière de D est pour l'exo suivant, je ne pense pas qu'il faille trop se fixer dessus). Supposons que f(x, y) soit continument différentiable par rapport à y dans D. Démontrer que f est localement l...
- par MaximusvcUcl
- 12 Mar 2022, 17:58
-
- Forum: ✯✎ Supérieur
- Sujet: Continue implique lipschitzienne
- Réponses: 2
- Vues: 242
Merci Mathelot pour ta réponse,
Comment tu trouves cette identification ?
Pour la norme uniforme je parle de
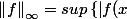 \right | : x\in [0,1]\right \})
- par MaximusvcUcl
- 15 Jan 2022, 12:18
-
- Forum: ✯✎ Supérieur
- Sujet: la n-ième dérivée
- Réponses: 10
- Vues: 418
Merci pour ta réponse, mais j'ai oublié de préciser que justement la dérivée en x=0 nous intéresse car on cherche la norme uniforme pour
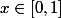
- par MaximusvcUcl
- 15 Jan 2022, 11:22
-
- Forum: ✯✎ Supérieur
- Sujet: la n-ième dérivée
- Réponses: 10
- Vues: 418
Bonjour à tous/toutes,
Je cherche la norme uniforme sur [0,1] de la n-ième dérivée de la fonction
=\frac{1}{1+2x})
.
Pour ce faire je pensais utiliser le fait que cette fct est équivalente à la série géométrique :
^n)
Que faire ensuite ?
Merci !
- par MaximusvcUcl
- 15 Jan 2022, 10:55
-
- Forum: ✯✎ Supérieur
- Sujet: la n-ième dérivée
- Réponses: 10
- Vues: 418
mathelot a écrit:bonsoir,
deux méthodes pour calculer la limite de
) méthode 1
méthode 1former et étudier le quotient
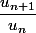
Qui donne 2/n+1 , et puis ?
- par MaximusvcUcl
- 14 Jan 2022, 19:00
-
- Forum: ✯✎ Supérieur
- Sujet: limite factorielle
- Réponses: 12
- Vues: 696
Bonjour,
J'aurais besoin d'aide pour calculer la limite en l'infini de la suite suivante :
!})
Je sais qu'elle vaut 0 mais comment le prouver ?
Merci d'avance !
- par MaximusvcUcl
- 14 Jan 2022, 18:40
-
- Forum: ✯✎ Supérieur
- Sujet: limite factorielle
- Réponses: 12
- Vues: 696
Imaginons qu'on te demande de montrer que la sphère est orientable, comment tu ferais ? D'ailleurs tant qu'on est sur l'orientation de la sphère, l'exo suivant est de montrer que l'application p:S^2->S^2 et qui a (x,y,z) renvoie (x,-y,z) a un degré de -1. Pour cela j'aimerais montrer que la différen...
- par MaximusvcUcl
- 29 Déc 2021, 09:41
-
- Forum: ✯✎ Supérieur
- Sujet: Paramétrisation de la bouteille de Klein
- Réponses: 8
- Vues: 581
Si tu cherche à savoir si deux cartes de la même zone sont orientées de la même façon, tu n'a rien à "inverser" : tu prend les images des bases canoniques par les différentielles de tes deux paramétrisation et tu regarde si elles orientent l'espace tangent de la même façon. Ah d'accord, j...
- par MaximusvcUcl
- 29 Déc 2021, 09:20
-
- Forum: ✯✎ Supérieur
- Sujet: Paramétrisation de la bouteille de Klein
- Réponses: 8
- Vues: 581
Salut, Je comprend pas bien grand chose : tu parle de QUELLE paramétrisation de la bouteille de Klein ? Et tu veut inverser quoi ? (Parce que "inverser une parametrisation", je vois pas bien ce que ça peut signifier . . .) Eh bien si je ne dis pas de bêtises, on dit qu'une variété M est o...
- par MaximusvcUcl
- 28 Déc 2021, 22:47
-
- Forum: ✯✎ Supérieur
- Sujet: Paramétrisation de la bouteille de Klein
- Réponses: 8
- Vues: 581