Limite factorielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 14 Jan 2022, 18:40
par MaximusvcUcl » 14 Jan 2022, 18:40
Bonjour,
J'aurais besoin d'aide pour calculer la limite en l'infini de la suite suivante :
!})
Je sais qu'elle vaut 0 mais comment le prouver ?
Merci d'avance !
Modifié en dernier par
MaximusvcUcl le 14 Jan 2022, 19:43, modifié 1 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Jan 2022, 18:53
par GaBuZoMeu » 14 Jan 2022, 18:53
Bonsoir,
Tu veux parler de la somme de cette série ? Elle n'est certainement pas nulle.
N'as-tu jamais rencontré la série de terme général
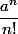
?
-
mathelot
 par mathelot » 14 Jan 2022, 18:56
par mathelot » 14 Jan 2022, 18:56
bonsoir,
deux méthodes pour calculer la limite de
) méthode 1
méthode 1former et étudier le quotient
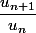 méthode 2
méthode 2utiliser la formule de Stirling qui donne un équivalent de n! quand n tend vers l'infini
^n)
on remplacera n par (n+1)
Modifié en dernier par mathelot le 14 Jan 2022, 18:59, modifié 2 fois.
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 14 Jan 2022, 18:56
par MaximusvcUcl » 14 Jan 2022, 18:56
Bonsoir,
Non je cherche vrmt à calculer lim u_n quand n tend vers l'infini
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 14 Jan 2022, 19:00
par MaximusvcUcl » 14 Jan 2022, 19:00
mathelot a écrit:bonsoir,
deux méthodes pour calculer la limite de
) méthode 1
méthode 1former et étudier le quotient
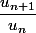
Qui donne 2/n+1 , et puis ?
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 14 Jan 2022, 19:02
par MaximusvcUcl » 14 Jan 2022, 19:02
aaah oui si ce terme est < 1 il ça converge vers 0 . ça me revient !
-
mathelot
 par mathelot » 14 Jan 2022, 19:02
par mathelot » 14 Jan 2022, 19:02
tu étudie la limite de la suite ou la limite de la série ?
La définition d'une série, c'est un couple de deux suites de terme général pour n entier:
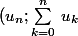)
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 14 Jan 2022, 19:43
par MaximusvcUcl » 14 Jan 2022, 19:43
Ah oui pardon j'ai fait une erreur en posant ma question, il s'agît de la limite de la suite ...
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 14 Jan 2022, 20:43
par tournesol » 14 Jan 2022, 20:43
!}=\frac{2}{n+1}\times\frac{2}{n}\times...\times\frac{2}{3}\times 2 \le 2\times(\frac{2}{3})^{n-1})
.
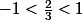
donc la limite est nulle .
Modifié en dernier par
tournesol le 14 Jan 2022, 22:44, modifié 1 fois.
-
mathelot
 par mathelot » 14 Jan 2022, 20:49
par mathelot » 14 Jan 2022, 20:49
}=\frac{2}{n+1}\times\frac{2}{n}\times...\times\frac{2}{3}\times 2 \le 2\times(\frac{2}{3})^{n-1})
.
il manque le factoriel à gauche de l'égalité
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 14 Jan 2022, 22:46
par tournesol » 14 Jan 2022, 22:46
Il manquait le factoriel à gauche de l'égalité .
Meilleurs voeux mathelot .
-
mathelot
 par mathelot » 14 Jan 2022, 23:03
par mathelot » 14 Jan 2022, 23:03
Merci. Bonne année2022 ,Tournesol.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Jan 2022, 21:03
par Ben314 » 15 Jan 2022, 21:03
Salut,
tournesol a écrit:!}=\frac{2}{n+1}\times\frac{2}{n}\times...\times\frac{2}{3}\times 2 \le 2\times(\frac{2}{3})^{n-1})
.
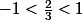
donc la limite est nulle .
Tu peut aussi majorer bêtement ton produit par
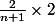
vu que tout les autres termes sont <1.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
.
donc la limite est nulle .