Je commence à faire cet exercice. Si vous pouvez m'aider, merci d'avance.
8 résultats trouvés
Revenir à la recherche avancée
Exercice du principe du module maximum
Calcule les valeurs maximale et minimale de  pour
pour
 , en fonction de
, en fonction de 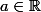 et
et  . L'idée est d'utiliser le principe du module maximum.
. L'idée est d'utiliser le principe du module maximum.
Je commence à faire cet exercice. Si vous pouvez m'aider, merci d'avance.
Je commence à faire cet exercice. Si vous pouvez m'aider, merci d'avance.
- 09 Nov 2021, 14:42
- Forum: ✯✎ Supérieur
- Sujet: Exercice du principe du module maximum
- Réponses: 1
- Vues: 296
Re: Exercice de surface de Riemann
GaBuZoMeu a écrit:Combien de déterminations possibles pour chaque racine carrée ? Combien de branches pour la fonction ?
Essaie de ne pas répondre au hasard.
Si vous vous référez à a)
Combien de déterminations possibles pour chaque racine carrée ? 2
Combien de branches pour la fonction ? 4
- 28 Oct 2021, 20:53
- Forum: ✯✎ Supérieur
- Sujet: Exercice de surface de Riemann
- Réponses: 14
- Vues: 698
Re: Exercice de surface de Riemann
Alors, pouvez-vous m'aider pour cet exercice ?
- 28 Oct 2021, 17:44
- Forum: ✯✎ Supérieur
- Sujet: Exercice de surface de Riemann
- Réponses: 14
- Vues: 698
Re: Exercice de surface de Riemann
tournesol a écrit:C'est peut être une coupure de Dedekind ???
Non, ce sont des coupes de branche dans le plan complexe.
- 28 Oct 2021, 15:17
- Forum: ✯✎ Supérieur
- Sujet: Exercice de surface de Riemann
- Réponses: 14
- Vues: 698
Re: Exercice de surface de Riemann
quelle est la coupure ? je n'ai pas bien compris, la demi droite verticale d''équation Re(z)=0 et Im(z) <= 1 En a) il est dit qu'il existe une branche coupée de z = -i à z = ∞. C'est ambigu. Pour préciser, vous pouvez prendre le demi-droite -i + R ^ + _ 0, ou tout autre demi-droite qui part de z = ...
- 28 Oct 2021, 13:06
- Forum: ✯✎ Supérieur
- Sujet: Exercice de surface de Riemann
- Réponses: 14
- Vues: 698
Re: Exercice de surface de Riemann
GaBuZoMeu a écrit:Combien de branches pour la fonction multivaluée de la question a) ?
Je pense 3 ou 4, je ne suis pas sûr.
- 27 Oct 2021, 19:53
- Forum: ✯✎ Supérieur
- Sujet: Exercice de surface de Riemann
- Réponses: 14
- Vues: 698
Re: Exercice de surface de Riemann
Je cherche un point de départ pour le faire car je ne sais pas par où commencer.
- 27 Oct 2021, 16:24
- Forum: ✯✎ Supérieur
- Sujet: Exercice de surface de Riemann
- Réponses: 14
- Vues: 698
Exercice de surface de Riemann
a) Si pour la fonction multivaluée f\left(z\right)=\sqrt{z-i}+\sqrt{z+i} les coupes de branches sont choisies comme les segments qui joignent z = i avec z = -i, et z = -i avec \infty , indique comment les 16 arêtes sont identifiées sur les quatre feuilles pour former leur surface de Riemann....
- 27 Oct 2021, 16:08
- Forum: ✯✎ Supérieur
- Sujet: Exercice de surface de Riemann
- Réponses: 14
- Vues: 698
- 8 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
