Forum de Mathématiques: Maths-Forum

quelle est la methode pour etudier la suite de terme general
Un=1-cos(Un-1)
merci

bonjour
voila plusieurs questions en vrac:
serait il possible d'avoir l'exemple d'une suite de cauchy

comment un espace peut etre ferme et non borne

un exemple d'une suite de cauchy qui ne converge pas en dim infinie

soit f,g \in C1([0,1], \Re ) soit le produit scalaire P(f,g)=f(0)g(0)+ \int f'(t)g'(t)dt l'intregrale est lineaire donc P est bilineaire est symetrique P(f,f)=f(0)^2)+ \int f'(t)^2dt \geq 0 donc P est positif P(f,f)=0 \Longleftrightarrow f(0)^2)+ \int f'(t)^2dt=0 est ce qu'on peut ecrire f(0)^2)=0 c...

desole klevia
merci beaucoup

et comment on montre le premier axiome

application N : * ->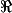
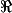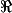
(x,y)-> sup|x+ty| t [0,1]

prouver que c'est une norme et dessiner la boule unite

A \in Mn x,y vecteurs colonnes f -> || produit scalaire = \sum [x][/i][y][/i] question : montrer que f est bornee sur la boule unite de E E bon constituee des vecteurs x tq ||x|| il existe r>0 tq norme(f(x))< r cad ||x||< 1 je comprend pas ce qu'il faut prouver