Forum de Mathématiques: Maths-Forum

Bonjour, j'ai déterminé la matrice inverse de P sans accroc, je rencontre un dernier soucis avec l'explicitation de la matrice 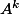je pense qu'il faut que je trouve une expression de 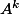par le calcul que je confirmerais par récurrence pensez vous que c'est la bonne méthode ?

Bonjour, non justement, j'ai regardé plusieurs fois mon cours et la notion de déterminant n'y figure pas...

Oui veuillez m'excuser, l'énoncer ne l'explicitait pas clairement ce n'est qu'en relisant que j'ai compris... Je rencontre un autre soucis sur cet exercice, on pose une matrice P telle que P=\begin{pmatrix} 11 & 1 & 1 \\ 5 & 0 & -1 \\ 4 & -1 & 0 \end{pmatrix} Montrer que P es...

Merci pour votre réponse, si on prend z=0 l'équation reste vraie mais d'après mon énoncé (qui se base sur des probabilités), on a d'abord posé x+y+z=1 à priori donc je pense qu'il existe une unique solution car si on prend z=1/5 on à bien x+y+z=1

Bonjour à tous, Je rencontre un problème avec un exercice sur les matrices: On me demande dans l'exercice si il existe un/plusieurs triplets (x,y,z) avec x,y,z \in \R* tels que : \begin{pmatrix} x \\ y \\ z \end{pmatrix}= A*\begin{pmatrix} x \\ y \\ z \end{pmatrix} avec A= \begin{pmatrix} 0,...

D'accord merci pour votre aide, dois-je procédé de la même façon pour Φ? l'argument que j'ai énoncé est correct pour la question 2 ?

Merci pour votre réponse, je ne vois pas comment calculer la limite en π/2 , je suis quelques peu perdu par l'énoncé, on nous dit g(x)=f(tan(x)) et g(x)=f(a) donc f(tan(π/2)=f(a) donc tan(π/2)=a mais comme vous l'avez dit tan n'est pas définie sur π/2...

Bonjour à tous ! J'ai un exercice à faire et je n'arrive pas à faire trois questions de celui-ci, voici l'énoncé: Soit a un réel, f: [a,+∞[→R continue sur [a,+∞[ et dérivable sur ]a,+∞[ avec lim f(x)= f(a) quand x→+∞ On admet qu'il existe un unique ϕ∈]-π/2,π/2[ tel que a=tan(ϕ), on définie g:[ϕ,π/2]...