Forum de Mathématiques: Maths-Forum

D'accord merci pour votre aide, je reviendrais vers vous si j'ai d'autres difficultés

Je trouve bien le même vecteur dirigeant la tangente (-0.811611690007821, 0.258651364883284) (j'avais fais une erreur en tapant la formule).
Je ne vois pas bien comment vous trouver le pas, pouvez vous me donner la formule que vous utilisez ?

Effectivement, j'ai oublié les carré dans la racine, j'ai en réalité une norme de 1.832305 et donc un lambda de 0.004576

Oui c'est ça,
je trouve que \vect{∆'} =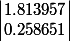 ce qui donne une norme de 1.439656
La norme de \vect{∆0} vaudra donc 0.006946 (∆0 représente )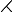
Est-ce que c'est bien ça (je ne suis pas sûr de moi) ?

Nous avons la fonction suivante : f(x,y) = (y−2)ye−x2x (1) Partie I 1. lire et faire le tutorial sur le logiciel Gnuplot et son utilisation en ligne. Tracer la surface de votre fonction f(x,y) dans le domaine x ∈ [−π,π] et y ∈ [π,π] a` l’aide de Gnuplot. Mettre le tracer dans le document avec les gr...

Le logo avec Image écrit à coté n'apparaît pas ?

Pour voir les images, il faut faire clic droit dessus et ouvrir l'image

Effectivement, je viens de refaire les calculs et je trouve que ce facteur s'annule en x=racine(2)/2 et en x=-racine(2)/2
Il y a donc 4 points critiques en x=-racine(2)/2 et y=1 ;en x=racine(2)/2 et y=1 ;en x=0 et y=2 ;en x=0 et y=0
Trouvez-vous la même chose ?

Je crois que j'ai enfin compris comment poster des images alors voici le sujet complet : https://postimg.cc/WtPPssR9 https://postimg.cc/TL0xZbHz https://postimg.cc/HJ4V3BbH https://postimg.cc/zbyY3fzM Pour ce qui est des points critiques je n'en trouve que 3 pour ma part en utilisant une technique v...

Bonjour, je suis en deuxième année d'un DUT génie mécanique et je dois rendre un DM pour la semaine prochaine. Je dois étudier la fonction suivante : f(x,y) = (y−2)*y*e^(−x²)*x Pour la première partie, je dois déterminer les points critiques exact de f ainsi que leur nature dans le domaine x ∈ [−π,π...