14 résultats trouvés
Revenir à la recherche avancée
Re: Trigo: période et intersections avec l'axe des x
Salut Pascal16 et merci pour ta réponse. Je crois que je comprends bien que la période peut être décalée par k , par contre je ne comprends toujours pas pourquoi ma solution pour l'intersection avec l'axe des x est incorrecte. Même en ajoutant ou en retirant \frac{\Pi }{3} à ma solution: \cos (2...
- 28 Avr 2019, 08:04
- Forum: ✎✎ Lycée
- Sujet: Trigo: période et intersections avec l'axe des x
- Réponses: 6
- Vues: 312
Re: Trigo: période et intersections avec l'axe des x
Merci Pascal16. Ce qui me chiffonne, c'est que mon bouquin me donne une autre solution pour les racines: x=\frac{5\pi}{18}+ k \frac {\pi}{3} J'ai le même souci si j'essaie la même recette pour la question suivante: trouver la période et l'intersection avec l'axe des x de \cos 2 x - 3 \pi : 2x - 3\pi...
- 27 Avr 2019, 20:59
- Forum: ✎✎ Lycée
- Sujet: Trigo: période et intersections avec l'axe des x
- Réponses: 6
- Vues: 312
Re: Trigo: période et intersections avec l'axe des x
Euh, en fait je soupçonne que la période est déjà inscrite en toute lettre dans mon équation ci-dessus (si elle est correcte...): 
Du coup, la période serait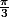
Suis je sur le bon chemin?
Du coup, la période serait
Suis je sur le bon chemin?
- 27 Avr 2019, 19:38
- Forum: ✎✎ Lycée
- Sujet: Trigo: période et intersections avec l'axe des x
- Réponses: 6
- Vues: 312
Trigo: période et intersections avec l'axe des x
Bonjour, toujours dans le même bouquin de Craats et Bosch, je cale sur cette question: trouver la période et les intersections avec l'axe des x de \tan (3x + \frac{1}{6}\pi) Je ne sais pas trop par quel bout m'y prendre. Est-ce que pour trouver les racines (intersections) je dois résoudre un...
- 27 Avr 2019, 19:20
- Forum: ✎✎ Lycée
- Sujet: Trigo: période et intersections avec l'axe des x
- Réponses: 6
- Vues: 312
Re: Trigonométrie, valeurs exactes de sin, cos et tan
J'avais oublié le "moins" en effet. Merci de m'avoir mis sur la bonne voie!
- 25 Avr 2019, 14:34
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Re: Trigonométrie, valeurs exactes de sin, cos et tan
Allons y: \sqrt{\frac{1}{2}(1-\frac{1}{2}\sqrt{3})} même dénominateur: = \sqrt{\frac{1}{2}(\frac{2}{2}-\frac{1}{2}\sqrt{3})} je distribue: = \sqrt{\frac{1}{2}-\frac{1}{4}\sqrt{3}} même dénominateur: = \sqrt{\frac{2}{4}-\frac{\sqrt{3}}{4}} = \frac{\sqrt{2-\sqrt{3}}}{\sqrt{4}} = \frac{...
- 25 Avr 2019, 11:10
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Re: Trigonométrie, valeurs exactes de sin, cos et tan
Je me permets de revenir sur l'exemple qui est donné dans le bouquin. Grâce à l'aide de chan79, j'ai pu le résoudre grâce à une addition, mais l'exemple du bouquin donne une "formule de l'arc double", selon laquelle: \cos \alpha = \pm \sqrt{\frac{1}{2} (1+ \cos 2 \alpha )} L'exempl...
- 24 Avr 2019, 19:44
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Re: Trigonométrie, valeurs exactes de sin, cos et tan
Un tout grand merci chan79, en suivant et décomposant pas à pas tes indications j'ai fini par me dépatouiller du premier exercice et à résoudre le second exercice (fort similaire) pour passer de
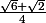 à la solution proposée par le livre de
à la solution proposée par le livre de 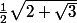
- 13 Avr 2019, 20:46
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Re: Trigonométrie, valeurs exactes de sin, cos et tan
D'ailleurs, un peu plus loin, j'ai un exercice similaire: calculer la valeur exacte de sin 7/12 pi Je procède en décomposant 7/12 en a = 1/3+ b = 1/4 (pour avoir des valeurs remarquables). Puis j'applique la formule sin (a+b) = sin a cos b + cos a sin b soit: \frac{\sqrt{3}}{2} \times \frac{\sqrt{2}...
- 13 Avr 2019, 20:03
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Re: Trigonométrie, valeurs exactes de sin, cos et tan
Hm... Je comprends l'égalité \frac{\sqrt{(\sqrt{6}-\sqrt{2})^2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4} mais je ne comprends pas l'égalité entre \frac{\sqrt{2-\sqrt{3}}}{2}=\frac{\sqrt{8-4\sqrt{3}}}{4} ni entre \frac{\sqrt{8-4\sqrt{3}}}{4}=\frac{\sqrt{(\sqrt{6}-\sqrt{2})^2}}{4} Merci de tout...
- 13 Avr 2019, 18:56
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Re: Trigonométrie, valeurs exactes de sin, cos et tan
cos(\frac{5\pi}{12})=cos(\frac{2\pi}{3}-\frac{\pi}{4})=\frac{-1}{2}\,\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}\,\frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4} Jusque là, je crois comprendre - mais comment passer de là à la solution: \frac{\sqrt{2-\sqrt{3}}}{2} J'ai sûrement des lacunes ...
- 13 Avr 2019, 15:54
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Re: Trigonométrie, valeurs exactes de sin, cos et tan
salut La ligne 3 me paraît fausse une méthode en utilisant la formule cos(a-b)=cos(a)cos(b)+sin(a)sin(b) cos(\frac{5\pi}{12})=cos(\frac{2\pi}{3}-\frac{\pi}{4})=\frac{-1}{2}\,\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}\,\frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4} ta méthode permet d'arr...
- 13 Avr 2019, 15:10
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Trigonométrie, valeurs exactes de sin, cos et tan
Bonjour, Je travaille en autodidacte avec le bouquin "Tout ce que vous avez appris et oublié en math" (de Jan van de Craats et Rob Bossch). Dans la partie trigonométrie, je suis coincé dans un exercice qui demande de donner les valeurs exactes de, p. ex., sin 1/8 pi, cos 1/12 pi, etc. Tant...
- 13 Avr 2019, 13:36
- Forum: ✎✎ Lycée
- Sujet: Trigonométrie, valeurs exactes de sin, cos et tan
- Réponses: 14
- Vues: 1056
Présentation
Bonjour, A l'âge vénérable de 52 ans, alors que je n'ai jamais fait d'autre travail que traducteur et que j'étais, pendant mes secondaires, dans une filière "langues modernes" qui ne prévoyait que 2 heures de math/semaine, voilà que je suis pris de l'envie de combattre mon inculture totale...
- 13 Avr 2019, 13:14
- Forum: ✌ Présentez-vous
- Sujet: Présentation
- Réponses: 1
- Vues: 347
- 14 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
