13 résultats trouvés
Revenir à la recherche avancée
- 04 Juin 2007, 14:10
- Forum: ✎✎ Lycée
- Sujet: Fonction définies sur R
- Réponses: 8
- Vues: 1223
- 03 Juin 2007, 10:54
- Forum: ✯✎ Supérieur
- Sujet: problème avec les matrices
- Réponses: 6
- Vues: 911
Bonjour!
Moi aussi j'ai un petit problème...
Quand je diagonalise une matrice 3x3 et que je trouve 2 valeurs propres a1 et a2 et que dimE1 = 2 et dimE2 = 1, comment s'écrit alors la matrice diagonale?
Est-ce :
a1 0 0
0 a1 0
0 0 a2
?
Moi aussi j'ai un petit problème...
Quand je diagonalise une matrice 3x3 et que je trouve 2 valeurs propres a1 et a2 et que dimE1 = 2 et dimE2 = 1, comment s'écrit alors la matrice diagonale?
Est-ce :
a1 0 0
0 a1 0
0 0 a2
?
- 03 Juin 2007, 10:41
- Forum: ✯✎ Supérieur
- Sujet: problème avec les matrices
- Réponses: 6
- Vues: 911
- 01 Juin 2007, 17:44
- Forum: ✯✎ Supérieur
- Sujet: séries de Fourier
- Réponses: 22
- Vues: 2243
Euh...un dernier truc, tu as marqué que sin(a(T/2 -t)) = sin(at) avec a=4kPI/T,
mais en développant je trouve
sin(a(T/2-t)) = sin(2kPI - at) = - sin(at)
mais en développant je trouve
sin(a(T/2-t)) = sin(2kPI - at) = - sin(at)
- 01 Juin 2007, 17:33
- Forum: ✯✎ Supérieur
- Sujet: séries de Fourier
- Réponses: 22
- Vues: 2243
- 01 Juin 2007, 17:19
- Forum: ✯✎ Supérieur
- Sujet: séries de Fourier
- Réponses: 22
- Vues: 2243
Euh...ouais sur le coup je suis nulle...
Désolée pour la perte de temps!
Mais grand merci pour m'avoir montrer ma grosse bourde....
Désolée pour la perte de temps!
Mais grand merci pour m'avoir montrer ma grosse bourde....
- 01 Juin 2007, 16:50
- Forum: ✯✎ Supérieur
- Sujet: séries de Fourier
- Réponses: 22
- Vues: 2243
Oui, je trouve l'intégrale égale à T/4 ce qui donne b(2k)=1, sauf erreur... En fait ça m'arrange pas que tu m'ais démonté mon hypothèse, parce que le prof l'a utilisée pour résoudre l'exercice... Il fallait que je prouve que la série de Fourier de f est de la forme : \sum \beta (k) sin((2k+1)(2PI/T)...
- 01 Juin 2007, 16:48
- Forum: ✯✎ Supérieur
- Sujet: séries de Fourier
- Réponses: 22
- Vues: 2243
oui y'a d'autres hypothèses sur f qui sont :
f(x) = f(T/2 -x)
et f(x) = - f(T/2 + x)
Je les ai pas mises parce que je croyais que le fait de vouloir h(PI/2 - x) = - h(x) ne dépendait que du sinus.
Est ce que ces conditions sur f t'éclairent? Je reste dans le flou...
f(x) = f(T/2 -x)
et f(x) = - f(T/2 + x)
Je les ai pas mises parce que je croyais que le fait de vouloir h(PI/2 - x) = - h(x) ne dépendait que du sinus.
Est ce que ces conditions sur f t'éclairent? Je reste dans le flou...
- 01 Juin 2007, 16:25
- Forum: ✯✎ Supérieur
- Sujet: séries de Fourier
- Réponses: 22
- Vues: 2243
Bonjour! La fonction est impaire de période T et on veut prouver que le coefficient bn=0 pour n=2k avec k>=1. On a : b(2k) = 4/T \int_{0}^{T/2} f(t)sin(2k2PIt/T)\, dt Mon prof pose alors h(t) telle que : h(t) = f(t) sin(2k*2Pi*t/T) et pour prouver que b(2k)=0 il montre que : h(PI/2 -...
- 01 Juin 2007, 16:12
- Forum: ✯✎ Supérieur
- Sujet: séries de Fourier
- Réponses: 22
- Vues: 2243
- 30 Mai 2007, 13:51
- Forum: ✯✎ Supérieur
- Sujet: Calculer une série
- Réponses: 24
- Vues: 1786
Ok donc :
1/(1-x) =
et 1/(1+x) =^n)
et finalement 1/(1+x²) =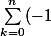^nx^2n)
Je galère un peu pour l'écriture donc c'est x à la puissance 2n.
J'ai juste?
1/(1-x) =
et 1/(1+x) =
et finalement 1/(1+x²) =
Je galère un peu pour l'écriture donc c'est x à la puissance 2n.
J'ai juste?
- 30 Mai 2007, 13:34
- Forum: ✯✎ Supérieur
- Sujet: Calculer une série
- Réponses: 24
- Vues: 1786
Bonjour,
Je suis en train de me casser la tête pour mes rattrapages d'analyse.
Je suis en L2 maths-physique et censée connaître le développement en série entière de 1 / (1+x²)...
Est ce que quelqu'un le connait?
Merci par avance
Je suis en train de me casser la tête pour mes rattrapages d'analyse.
Je suis en L2 maths-physique et censée connaître le développement en série entière de 1 / (1+x²)...
Est ce que quelqu'un le connait?
Merci par avance
- 30 Mai 2007, 13:06
- Forum: ✯✎ Supérieur
- Sujet: Calculer une série
- Réponses: 24
- Vues: 1786
- 13 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
