Forum de Mathématiques: Maths-Forum

IntegerX a écrit:Oui c'est la bonne solution.
Après pour arriver à cette conclusion tu peux faire un tableau de signes, c'est plus visuel et ça te permet d'éviter certaines erreurs.

D'accord j'y penserai la prochaine fois en tout cas merci beaucoup pour votre aide et votre attention !

IntegerX a écrit:Le calcul est juste, mais il y a un petit problème pour les solutions.
Tu cherches les solutions telles que le produit soit négatif, donc les deux facteurs ne doivent pas être du même signe.

Ah c'est x>-3 non ?
Et donc S=]-3 ; 1[

???

C'est exactement comme ce que tu avais fait, sauf qu'il faut remplacer les 4x par des 2x quand tu factorises :) Je pense donc avoir trouver et se serait : 4xcarré - (x-3)carré <0 [2x+(x-3)][2x-(x-3)]<0 2x+x-3<0 et 2x-x+3<0 3x-3<0 et x+3<0 3x<3 et x<-3 x<1 et x<-3 S= ]- infini ; 1[ ??

D'accord merci beaucoup

pascal16 a écrit:As-tu fait le tableau de variations ?



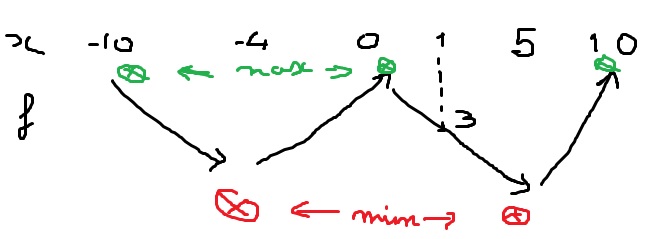
en rouge : les seuls endroits où f peut atteindre un minimum
en verte : là où elle peut atteindre un maximum

Donc si je comprend bien -2<f(x)<0

Oui, je l'ai fait mais je n'ai pas penser comme cela mais c'est vrai maintenant ça paraît logique merci !

Désolé mais je n'ai pas compris

Bonjour, je n'arrive pas à réaliser la question 1) de mon exercice, pouvez vous m'aider? Voici l'énoncé de mon exercice:  Soit f une fonction vérifiant:  •f est définie sur [-10;10]  •f est croissante sur [-4;0] et sur [5;10] puis f est décroissante dur [-10;-4] et sur [0;5]  •les antécédents par f ...

Bonjour, je dois réaliser le meilleur encadrement de f(x) lorsque celui ci appartient à [-4 ; 5] mais je ne sais pas comment m'y prendre

D'accord mais alors le résultat change ?!

IntegerX a écrit:Si c'est bien pour utiliser a² - b²=(a-b)(a+b), sauf que ici 4x² = (2x)² donc notre a = 2x

Je suis perdu, je n'arrive pas à la résoudre

D'accord merci

IntegerX a écrit:Si c'est bien pour utiliser a² - b²=(a-b)(a+b), sauf que ici 4x² = (2x)² donc notre a = 2x

Ah oui d'accord merci

Re bonjour Pour la 2nd j'ai trouvé 4xcarré - (x-3)carré <0 [4x+(x-3)] [4x-(x-3)] <0 4x+x-3 <0 et 4x-x+3<0 5x-3 <0 et 3x+3<0 5x<-3 et 3x<3 x<-3/5 et x<1 S=]-infini ; 1[ Pouvez vous me dire si c'est exacte Merci Je suppose que quand tu écris 4xcarré c'est 4x² et pas (4x)² Donc  4x² - (x-3)² = (2x)² -...

IntegerX a écrit:Fais aussi attention quand tu as 5x-3 < 0, ça revient à 5x < 3 et non -3 (idem pour 3x+3 < 0).

Oui merci il me semblait aussi

Re bonjour Pour la 2nd j'ai trouvé 4xcarré - (x-3)carré <0 [4x+(x-3)] [4x-(x-3)] <0 4x+x-3 <0 et 4x-x+3<0 5x-3 <0 et 3x+3<0 5x<-3 et 3x<3 x<-3/5 et x<1 S=]-infini ; 1[ Pouvez vous me dire si c'est exacte Merci Je suppose que quand tu écris 4xcarré c'est 4x² et pas (4x)² Donc  4x² - (x-3)² = (2x)² -...

Re bonjour
Pour la 2nd j'ai trouvé
4xcarré - (x-3)carré <0
[4x+(x-3)] [4x-(x-3)] <0
4x+x-3 <0 et 4x-x+3<0
5x-3 <0 et 3x+3<0
5x<-3 et 3x<3
x<-3/5 et x<1
S=]-infini ; 1[

Pouvez vous me dire si c'est exacte
Merci

Bon et bien merci beaucoup

J'en ai une 2nd à effectué, celle ci

4xcarré-(x-3)carré <0

Et je pense l'effectué avec l'identité remarquable
(acarré-bcarré)