Merci pour les explications
33 résultats trouvés
Revenir à la recherche avancée
Re: valeur propre
Oui mais avec l'énoncé que j'ai, je peux prendre le vecteur u comme vecteur propre de  de telle sorte que
de telle sorte que =\lambda u) et donc dire que u est dans le noyau de l'endomorphisme
et donc dire que u est dans le noyau de l'endomorphisme 
Merci pour les explications
Merci pour les explications
- 25 Aoû 2018, 14:49
- Forum: ✯✎ Supérieur
- Sujet: valeur propre
- Réponses: 10
- Vues: 457
Re: valeur propre
Ce que je dis n'est pas correct alors...
- 25 Aoû 2018, 12:18
- Forum: ✯✎ Supérieur
- Sujet: valeur propre
- Réponses: 10
- Vues: 457
- 25 Aoû 2018, 12:09
- Forum: ✯✎ Supérieur
- Sujet: valeur propre
- Réponses: 10
- Vues: 457
Re: valeur propre
Le vecteur u serait plus convenable alors
- 25 Aoû 2018, 11:53
- Forum: ✯✎ Supérieur
- Sujet: valeur propre
- Réponses: 10
- Vues: 457
Re: valeur propre
Dans ce cas le noyau c'est les antécédents de O_{E} dans E Ça veut dire que le noyau de \varphi -\lambda Id_{E} n est pas nulle, donc l'endomorphisme \varphi -\lambda Id_{E} est non injectif donc Ker ( \varphi -\lambda Id_{E} ) n'est pas réduit à vecteur nulle et si je remplace dans votre "énon...
- 25 Aoû 2018, 09:28
- Forum: ✯✎ Supérieur
- Sujet: valeur propre
- Réponses: 10
- Vues: 457
valeur propre
Bonjour, Dans un exercice, on me demande de justifier que \lambda est une valeur propre de \varphi si et seulement si ker(\varphi-\lambda*Id_{E})\neq {0_{E}} . Je sais qu'on appelle valeur propre d'un endomorphisme \varphi , un réel \lambda telqu'il existe un vecteur u non nul tel que \varph...
- 24 Aoû 2018, 17:48
- Forum: ✯✎ Supérieur
- Sujet: valeur propre
- Réponses: 10
- Vues: 457
Re: Division Euclidienne
Non, je n'avais pas compris mais mon problème est résolu, j'ai compris comment faire.
Merci quand même !
Merci quand même !
- 20 Aoû 2018, 14:00
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Re: Division Euclidienne
Ah bah oui suis-je bête, pourquoi n'y ai-je pas pensé avant...
mais en écrivant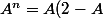+2^{n}*(A-1)^{2}+n(2-A)(A-1)) , je n’obtiens pas comme vous..
, je n’obtiens pas comme vous..
Merci
mais en écrivant
Merci
- 19 Aoû 2018, 19:25
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Re: Division Euclidienne
Je trouve le même résultat (heureusement) en passant par le système d'équation mais ça prend tellement plus de temps... Je sais d'après l'énoncé de mon exercice que P(A)=0 et je dois en déduire une expression de A^{n} comme combinaison linéaire de A^{2}, A, I_{3} Si j'écris : P(A)=0 ...
- 19 Aoû 2018, 17:08
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Re: Division Euclidienne
Merci pour toutes ces explications, même si je ne pense pas que cette technique soit adaptée à mon niveau
- 19 Aoû 2018, 16:34
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Re: Division Euclidienne
J'ai une autre question, est-ce que ça change quelque chose de changer les polynômes de places et par exemple de mettre (2-x)x) ?
?
- 19 Aoû 2018, 15:31
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Re: Division Euclidienne
Bonjour, "Ca" me dit que A(1)=R(1), A(2)=R(2), A'(1)=R'(1) dans ce cas R(X)=(2-X)X+2^{N}*(X-1)^{2}+N*(2-X)(X-1) et c'est les seuls polynômes vérifiant les 3 trucs que je viens de trouver ! YEESS...
- 19 Aoû 2018, 15:12
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Re: Déduction
Ah oui, bien sur !
Merci beaucoup
Merci beaucoup
- 18 Aoû 2018, 16:17
- Forum: ➳ Orientation
- Sujet: Déduction
- Réponses: 2
- Vues: 573
Re: Division Euclidienne
Ok, merci beaucoup pour vos réponses !
Par contre, je ne comprend pas comment vous obtenez, r(x) sous la forme générale ?
Par contre, je ne comprend pas comment vous obtenez, r(x) sous la forme générale ?
- 18 Aoû 2018, 16:06
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Déduction
Bonjour,
On me demande dans un exercice de déduire l'expression de la température en fonction du temps à partir de cette formule :
En intégrant je trouve :

et à partir de là je ne vois pas comment faire...
Merci d'avance
On me demande dans un exercice de déduire l'expression de la température en fonction du temps à partir de cette formule :
En intégrant je trouve :
et à partir de là je ne vois pas comment faire...
Merci d'avance
- 18 Aoû 2018, 10:08
- Forum: ➳ Orientation
- Sujet: Déduction
- Réponses: 2
- Vues: 573
Division Euclidienne
Bonjour, Je cherche à trouver le reste du division euclidienne mais je bloque... Ma division est la suivante : \frac{X^{N}}{P} avec P=X^{3}-4X^{2}+5X-2 Je pensais factoriser P pour simplifier la division mais ça ne m'aide pas énormément... En factorisant P dans R[X], j'obtiens P=(X-2)(X-...
- 17 Aoû 2018, 16:15
- Forum: ✯✎ Supérieur
- Sujet: Division Euclidienne
- Réponses: 15
- Vues: 673
Re: Matrice de passage
Merci beaucoup aviateur, pascal16 et LB2
- 17 Aoû 2018, 14:11
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage
- Réponses: 6
- Vues: 320
Matrice de passage
Bonjour, Je coince sur une question, mon énoncé est le suivant ; On considère un R-espace vectoriel E quelconque muni d'une base \beta=(e_{1},e_{2},e_{3}) Soit \varphi l'endomorphisme dont la matrice dans la base \beta est : A=\frac{1}{2}\begin{pmatrix} 8 & -2 & -2\\ 3 & 1 & ...
- 16 Aoû 2018, 22:15
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage
- Réponses: 6
- Vues: 320
Re: intégration
Bonjour et merci...
- 06 Aoû 2018, 09:02
- Forum: ✯✎ Supérieur
- Sujet: intégration
- Réponses: 27
- Vues: 905
Re: intégration
C'est souvent aussi simple lorsque les questions commencent par en déduire ? On a donc : 0<\frac{n}{n+3}I_{n-1}\leq I_{n}\leq I_{n-1} Je dois montrer que I_{n-1} ~+infini I_{n} - j'imagine que la vague avec le + l'infini correspond à équivalent à lorsque n tend vers plus l'infini... est-ce vrai ? -E...
- 05 Aoû 2018, 21:07
- Forum: ✯✎ Supérieur
- Sujet: intégration
- Réponses: 27
- Vues: 905
- 33 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
