Forum de Mathématiques: Maths-Forum

Merci Elias j'ai déjà fait cette exercice

Merçi pour votre aide

Soit (X,d) un espace métrique f et g deux applications de X dans X. On dit que f et g sont compatible si pour toute suite x_{n} de X tel que \lim d(f(x_{n}),u)=0 et \lim d(g(x_{n}),u)=0 pour certain u\in X alors \lim d(f(gx_{n}),g(f(x_{n}))...

Si, car je n'ai que qui converge vers 0 et pour la deuxième i.e je n'ai aucun idèe sur cette suite là comment peut on montrer que si 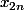est de cauchy alors l'est aussi

Merç pour votre réponse j'ai une tout petite remarque si l'appliaction d ne vérifie pas la condition de la symètrie comment on peut obtenir le résultat dans la cas où p et q sont impairs

@ mathelot oui c'est bien ça

$x_{2n}$ la sous suite de terme paire

bonsoir,
Si $x_{2}$ est une suite de CAUCHY AVEC $d(x_{n},x_{n+1})$ converge vers 0 alors la suite (x_{n}) est de Cauchy . Avec d une véréfie les propriètés d'une distance sauf elle est pas symétrique. J'arrive pas à démontrer ça quelqu'un peut m'aider et merçi