Forum de Mathématiques: Maths-Forum

Merci à vous deux j'ai pourtant ré-essayé une demi dizaine de fois hier mais rien ne marchait !!
C'est très frustrant x)

Merci !

Bonjour pour un DM j'ai: Un plan: (IJK)\begin{cases} & x=1+1,5t+2t' \\ & y=1-0,5t-4t' \\ & z=-1-1,5t+4t' \end{cases} Et une droite: (AD)\begin{cases} & x=-1+6t'' \\ & y=-2t'' \\ & z=2+2t'' \end{cases} Je dois montrer qu'ils ...

Personnellement, si vraiment tu veux un moyen rigoureux il te suffit de dire au début de l'exercice Je ne suis vraiment pas sur que mon prof l'accepte, il est très "académique" Au fait tu n'as pas répondu sur ton autre sujet sur les intégrales. Oui, désolé, j'ai du lâcher ça, je le faisai...

Eheh, tu parles en tant que matheux, mais crois moi que quand on te pose un exercice avec 20 polynomes à résoudre en 10 minutes.. ^^

Donc, les maths (cette si veille et parfaite science) ne donne aucun moyen d'exprimer ça plus concisement ?!
Je suis vraiment surpris..

Merci en tout cas !

Bonjour, Je suis souvent amené à calculer des racines de polynomes avec le discriminant de cette manière: x_{1}=\frac{-b-\sqrt{\Delta }}{2a}=x x_{2}=\frac{-b+\sqrt{\Delta }}{2a}=y (Où delta positif) Mais c'est très long et pas très esthétique alors je l'écrivais comme ça: x_{1,2}=\frac{-b\pm\sqrt{\D...

Bonjour, Je suis sur les intégrales, sur comment calculer une primitive à partir de l'intégrande; Pour une intégrande très simple j'y arrive: f(x) = 3 F(x)=\int_{0}^{x}{f(x)dx}=f(x)\int_{0}^{x}{dx}=f(x)x=3x Mais avec une intégrande un tout petit peux plus comp...

Ahah oui, mais si je continue, je suis contre productif x) Ducoup ça me fait 2.5 = x + 1/x = 2.5x = x + 1 = 1.5x = 1 = x = 1/1.5 = 0.6 et pour 5.2 j'ai 1/4.2 = 0.23 Ce qui est proche des deux racines 0.2 et 0.5 est-ce correcte ? ou j'ai encore fait des erreures ? Merci ! PS: C'est plus un commentair...

Pour u j'ai trouvé 2.5 et 5.2 mais il vas falloir que je trouve une maniere d'extraire x de u = x + (1/x) !

Comme je suis pas futé je vais switcher sur un corpus sinon je surchaffe ! x)

Merci beaucoup !

Hum oui..

Mais du coup ça donne est egal à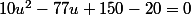

Mais quand je calcul les racines à partir du discriminant, elle ne résolvent pas l'équation

Roh oui désolé ^^ !

Ducoup on peux dire que ça nous donne serait égal à ?

Ah oui merci, c'est malin je l'avais pas vus !

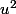vaudrait

donc on peux faire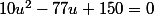 ce qui se ramenne à un polynome de second degré !

Merci !

Tiruxa47 a écrit:Bonjour

Il ne doit pas y avoir à la fois des x et des u dans la même équation
On a
10(x²+1/x²) -77(x+1/x)+150=0

Ensuite effectue le changement

Merci, mais je ne vous pas trop comment on arrive a ce resultat

Lostounet a écrit:

Akrone a écrit:puis de démontrer que ce qui est prouvé par l'identité

Euh..Je ne connais pas cette identité je ne l'ai jamais vue. Tu es sûr?

Désolé, c'est corrigé

Bonjour, Je suis bloqué sur la résolution du polynome de 4ème degré : (E): 10x^4-77x^3+150x^2-77x+10=0 En effet, on demande de diviser l'équation par x², ce qui fait (E): 10x^2-77x+150-77\frac{1}{x}+10\frac{1}{x^2}=0 puis de démontrer que x^2+\frac{1}{x^2}=(x+\frac{1}{x})^2-2...