Forum de Mathématiques: Maths-Forum

WillyCagnes a écrit:Bsr
Remplace le + par ^ dans ta formule
https://fr.m.wikipedia.org/wiki/Formule_de_Gibbs

C'est fait, je m'excuse.

Bonsoir à tous, Je voulais démontrer la formule de Gibbs : \vec{u} \wedge (\vec{v} \wedge \vec{w})= ( \vec{u}. \vec{w}). \vec{v} - ( \vec{u}. \vec{v}). \vec{w} Sachant que dans mon cours cette formule est donné avant le théorème de l'expression analytique du produit vectoriel...

Bonsoir a tous, On me demande de répartir 9 boules dans 4 cases et de calculer la probabilité : A : aucune case ne soit vide B : 5 boules dans une case, 3 dans une autre case, 2 dans celle qui reste?? J'ai fait : Card (univers) = 4^9 Card (A) = 1^5 * 1^4 * 1^2 Card (B) = 1^9 * 1^8 * 1^7 * 1^6 Mais j...

On peut pas dire plutot que la suite Un est majorée par n? Donc Un<n <=> -Un>-n On a U_2n - Un > 1/2 <=> U_2n - n > 1/2 <=> U_2n > 1/2 + n On a 1/2 + n tend vers + l'infini , donc la suite est divergente ? Bonsoir, Tu supposes que la suite Un est majorée par n (ne pas oublier : quelque soit n), et ...

Bonjour Ou alors tu en déduis que V_{2^n}-V_1>=n\times 1/2 Salut, On peut pas dire plutot que la suite Un est majorée par n? Donc Un<n <=> -Un>-n On a U_2n - Un > 1/2 <=> U_2n - n > 1/2 <=> U_2n > 1/2 + n On a 1/2 + n tend vers + l'infini , donc la suite est divergente ?

chan79 a écrit:salut
Suppose que admette comme limite un réel a.
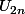
Que dire de et de ?

Bonsoir,
donc la différence doit être égale à 0 ?
Or c'est >=1/2 , donc la suite est divergente ?

Bonjour à tous, Je m'intéresse en particulier à étudier la convergence de la somme des 1/k , k allant de k=1 à k=n j'ai montré donc que la suite était croissante et que U_2n - U_n > 1/2 (l'énoncé était guidé) mais après je sais pas comment procéder, sachant que je n'ai pas le droit d'utiliser les su...

Bonjour, Cela doit être : S_n = 1+ 1+ \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + ... +\frac{1}{n!} pour la minoration par 2. Pour la majoration par 3, on voit bien que la récurrence ne va pas marcher. On ne sait pas sommer cette suite, mais on sait sommer les suites géométriques. Donc penser à ma...

Bonsoir à tous, Je dois montrer que ma suite : S_n = 1+ \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + ... +\frac{1}{n!} 1)est bornée par 2 et 3 2) convergente vers une limite qu'on précisera. 3) Etudier la convergence des suites : U_n=1+ \frac{1}{\sqrt2} + \frac{1}{\sqrt3} + \frac{1}{\sqrt4} + ... +\...

Bonjour à tous, Je bloque sur mon exercice sur les dénombrements : Un sac contient : cinq boules rouges numérotés 0,0,1,2,2 trois boules blanches numérotés 0,1,2 deux boules jaunes numérotés 0,4 on tire successivement sans remise quatre boules du sac Dénombrer les tirages donnant: a) deux boules bla...