16 résultats trouvés
Revenir à la recherche avancée
Re: Problème de minimisation
l'ensemble E admet une condition de majoration seulement donc la borne inf reste inchangée
- 26 Fév 2017, 15:50
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
oui effectivement. Je ne vois pas comment faire pour justifié l'égalité
- 26 Fév 2017, 14:24
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
mais ça me paraît triviale de dire que E est inclus de 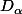
- 26 Fév 2017, 12:33
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
De plus E est inclu dans
- 26 Fév 2017, 11:43
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
Le fait que E soit fermé borné implique directement que la borne inf est atteinte?
- 26 Fév 2017, 11:02
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
oui je comprends, Je pensais simplement que le but de la question (1) était d'établir l'inégalité afin de pouvoir justifier par la suite que la borne inf était atteinte ce qui aurait été possible justement si J_A(x_0)=m.
- 25 Fév 2017, 19:34
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
de là j'en déduit que
donc si
- 25 Fév 2017, 19:10
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
- 25 Fév 2017, 17:37
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
(2) =\langle x,Ax\rangle \ge m \prod_{k=1}^n x_{k}^{2\alpha _k / |\alpha |})
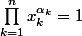 pour
pour 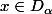 donc
donc
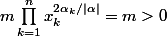
d'ou >0)
d'ou
- 25 Fév 2017, 12:38
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
oui, en effet merci la question (2) est assez évidente. pour la (3) le lagrangien est L(x,\lambda)=\langle x,Ax\rangle - \lambda (\prod_{k=1}^n x_{k}^{\alpha _k} - 1) \nabla L = 0 <=> 2Ax-\lambda(\alpha_i x_{i}^{\alpha_{i}-1} . \prod_{k=1,k \ne i}^n x_{k}^{\alpha _k}) =0 avec...
- 25 Fév 2017, 11:54
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
il reste a montrer que
- 24 Fév 2017, 21:26
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
D'accord j'ai compris!
La deuxième partie de la question 1 que j'ai fais est juste ou c'est une erreur d'utiliser le faite que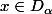 ?
?
La deuxième partie de la question 1 que j'ai fais est juste ou c'est une erreur d'utiliser le faite que
- 24 Fév 2017, 18:39
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
oui, on peut parler de valeur propre je suis en 1ere année de master en maths, je connais également la notion de norme equivalentes.
- 24 Fév 2017, 17:50
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
c'est le quadrant des n-uplet (x_1,...,x_n) à coefficient positif tous non nul. La notion de quadrant je ne comprends pas vraiment à quoi ça correspond. c'est vrai que A_{ij} peut être négatif mais \langle x,Ax\rangle = \sum A_{ij} x_i x_j donc ça peut être négatif et m\|x\|^{2}_{\infty} est...
- 24 Fév 2017, 17:17
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Re: Problème de minimisation
Oui, désolé j'ai en effet oublié quelques infos et fait des fautes de recopiages, c'est corrigé.
- 24 Fév 2017, 15:30
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
Problème de minimisation
Bonjour, je rencontre des difficultés à résoudre le problème suivant: soient n \ge 2 , (x_1...x_n) \in R^{n}_{++} , \alpha=(\alpha_1...\alpha_n) \in R^{n}_{++} R^{n}_{++} est le quadrant des n-uplet (x_1,...x_n) à coefficient positif tous non nul et A une matrice symétrique c...
- 24 Fév 2017, 14:49
- Forum: ✯✎ Supérieur
- Sujet: Problème de minimisation
- Réponses: 33
- Vues: 1343
- 16 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
