Bonjour, merci pour la réponse tout d'abord,
Et justement cette formule de (Zn) n'est plus bonne à partir de Z2 ...
14 résultats trouvés
Revenir à la recherche avancée
- 19 Fév 2017, 16:44
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Désolé de rouvrir ce post, mais en revenant à mes résultats, j'ai trouvé une erreur.. J'avais trouvé 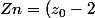^{2}) (puissance n) +2
(puissance n) +2
mais après vérification, ça ne marche pas pour le z0 donné..
mais après vérification, ça ne marche pas pour le z0 donné..
- 19 Fév 2017, 16:11
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Ah.. Je réfléchis mais j'ai du mal à trouver une limite sachant qu'elle dépendrait de 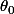 ..
..
Apparemment la suite Zn ne converge pas, mais j'ai eu l'impression que l'exercice nous amenait à montrer que la suite Zn tend vers 2 ..
Apparemment la suite Zn ne converge pas, mais j'ai eu l'impression que l'exercice nous amenait à montrer que la suite Zn tend vers 2 ..
- 16 Fév 2017, 23:59
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
La suite est géométrique de raison q=2, donc croissante?
- 16 Fév 2017, 23:36
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Ah oui.. Donc 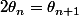 ?
?
Et pour la dernière question je pense qu'il faut chercher la limite de Zn, indirectement donc celle de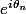 ? Mais je ne sais pas comment m'y prendre
? Mais je ne sais pas comment m'y prendre
Et pour la dernière question je pense qu'il faut chercher la limite de Zn, indirectement donc celle de
- 16 Fév 2017, 22:39
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
J'ai relu les propriétés des arguments, mais je ne vois pas d'où partir pour exprimer 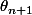 en fonction de
en fonction de 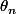 ..
..
- 16 Fév 2017, 22:21
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Pour la question 5)c), j'ai trouvé: 
Et pour la question suivante, par déduction ce serait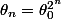 ?
?
Et pour la question suivante, par déduction ce serait
- 16 Fév 2017, 19:19
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
La question 5)a) me dit que |zn-2|=1, et je sais qu'un complexe de module 1 peut s'écrire: Z=e^{i\theta} Donc.. Z_{n}-2=e^{i\theta} ? C'est bon je pense avoir compris: en énoncant l'écriture d'un complexe de module 1, je peux donc utiliser ce qui est trouvé dans la question d'avant pour montrer que ...
- 16 Fév 2017, 18:13
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Bonjour, j'ai réussi à avancer dans l'exercice, je bloque un peu pour la question 5)b), je ne sais pas d'où partir pour démontrer l'existence du réel 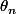 ..
..
- 16 Fév 2017, 17:54
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Oulà pardon c'est moi qui ait fait une erreur en recopiant, j'ai trouvé : 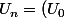^2) puissance n
puissance n
- 16 Fév 2017, 16:09
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Oui c'est bien ce que j'ai trouvé.. 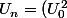^n)
- 16 Fév 2017, 15:22
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
C'est bon j'ai enfin compris.
J'ai donc trouvé: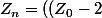^2)^n +2)
C'est bien ça?
J'ai donc trouvé:
C'est bien ça?
- 16 Fév 2017, 14:50
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
Re: DM - Suites / Complexes
Bonjour, merci pour vos réponses 
Donc si j'ai bien compris, je pose Un = Zn - 2, et j'effectue une récurrence avec comme hypothèse =Un^2) ?
?
Donc si j'ai bien compris, je pose Un = Zn - 2, et j'effectue une récurrence avec comme hypothèse
- 16 Fév 2017, 12:54
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
DM - Suites / Complexes
Bonjour, je suis en terminale S et voici le DM qui me pose problème : https://image.noelshack.com/minis/2017/07/1487208190-14872081083151135842389.png J'ai fait les questions 1), 2) et 3)a) et je ne sais pas du tout comment procéder pour la suite de l'exercice. Merci d'avance pour l'aide que vous po...
- 16 Fév 2017, 02:25
- Forum: ✎✎ Lycée
- Sujet: DM - Suites / Complexes
- Réponses: 31
- Vues: 1541
- 14 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
