Forum de Mathématiques: Maths-Forum

Non tu as du te tromper dérive déjà

Non absolument pas ! Je te donne la formule vu que tu ne semble pas la connaitre . (\sqrt{f})' = \frac{f'}{2\sqrt{f}} Dit en français : La dérivé d'une fonction qui est sous une racine carrée est la dérivée de cette fonction divisée par 2 fois la racine carrée de cette fonction. Main...

As-tu essayé de chercher ? La première question est simple écrit l'expression de en fonction des autres puis aides toi des nombreuses informations que l'on te donne

Tu as du voir dans ton cours quelle était la dérivée de

Ton delta est bon c'est bien

Donc tu as : , et

Bonjour,

Attention il y a dès la première question une erreur dans l'une de tes racines recalcule le tout !

Bonjour je t'aide pour la toute première : Tu as : \vec{BF} = \frac{3}{2}\vec{BD} Utilises la relation de Chasles pour déduire : \vec{BF} = \frac{3}{2}(\vec{BA}+\vec{AD}) Puis tu as \vec{AB} = \vec{AD}-\vec{AC} ce qui équivaut à \vec{BA} = -\vec{AD}+\vec{AC} Tu remplaces \vec{BA} tu développ...

Bonjour,

As-tu ou ?

Oui en fait je ne l'ai pas mise car g_{n}(x) = f_{n}(x) + e^{-x}\frac{x^{n}}{n!} ou f_{n}(x) est un peu compliqué mais on me donne sa dérivée dans l'énoncé c'est : f'_{n}(x) = -e^{-x}\frac{x^{n}}{n!} Du coup j'en ai déduit que g'_{n}(x) = f'_{n}...

Ok !
Et sur ! car

Donc est positive sur donc est croissante sur ?

C'est bien sa ?

Merci pour ta réponse rapide !

Ce n'est pas une erreur de frappe ce sont bien les mêmes termes mais cela ne m'aide pas

Bonne idée de factoriser par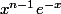 je n'y avais pas pensé !

Du coup si je ne me suis pas trompé sa me donne :

Bonjour ! J'ai besoin d'étudier les variations d'une fonction g_n(x) ou n\geq 2 , j'ai donc dérivé cette fonction ce qui me donne : \large g'_{n}(x) = \frac{-e^{-x}x^{n}-e^{-x}x^{n}+e^{-x}nx^{n-1}}{n!} N.B. : Je doit étudier les variations de g_{n}(x) sur l'intervalle [0;...