Etude de signe

[JulienHJ54789]

Bonjour !

J'ai besoin d'étudier les variations d'une fonction ou , j'ai donc dérivé cette fonction ce qui me donne :



N.B. : Je doit étudier les variations de sur l'intervalle

Je doit donc maintenant étudier le signe de cette expression pour en déduire les variations mais je n'arrive pas à suffisamment factoriser pour pouvoir faire mon tableau de signe puis de variations
Merci à ceux qui m'aideront !

[samoufar]

Bonjour,

D'abord les deux premiers termes du numérateur sont les mêmes (sauf en cas de faute de frappe).

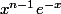
Essaie de factoriser le numérateur par , qui est un terme positif.

[JulienHJ54789]

Merci pour ta réponse rapide !

Ce n'est pas une erreur de frappe ce sont bien les mêmes termes mais cela ne m'aide pas

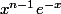
Bonne idée de factoriser par je n'y avais pas pensé !

Du coup si je ne me suis pas trompé sa me donne :

[samoufar]

Donc on a , le terme de gauche étant... positif, donc inutile dans la détermination du signe de .

[JulienHJ54789]

Ok !
Et sur ! car

Donc est positive sur donc est croissante sur ?

C'est bien sa ?

[Ben314]

Salut,
Vu que les primitives de sont tout sauf triviales, j'aurais un tout petit peu tendance à me demander si ta dérivée est correcte ou pas.
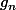
Peut-tu nous donner l'expression de la fonction de départ, juste pour voir ?

[JulienHJ54789]

Oui en fait je ne l'ai pas mise car ou est un peu compliqué mais on me donne sa dérivée dans l'énoncé c'est :

Du coup j'en ai déduit que
Et ça m'a donné l'expression dont je souhaite étudier le signe (dans mon premier message) pour connaitre les variations de sur