Forum de Mathématiques: Maths-Forum

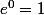
laetidom a écrit:Effectivement, maintenant le résultat fait bien , et comme tu as réussi à le faire tout est donc ok Laaure ! Bonne soirée.

Oui c'est bon. Merci pour ton aide !
Bonne soirée à toi aussi.

Pas de souci !
Alors voilà le bon énoncé :

f(x) = e^x + e^-x /2
g(x) = e^x + e^-x /2

Démontrer que pour tout nombre réel x, on a : (f(x))² - (g(x))² = 1.

Oui bien sur je le donne après là je vais en cours.
Bonne journée également

Bonjour,
J'ai demandé ma prof de maths et elle s'est trompé dans l'exercice ! (PS: zygomatique → je sais très bien lire merci !!! C'était tout simplement la prof qui s'était trompé !)
Merci pour ton aide laetidom. J'ai de ce fait réussi à faire l'exercice.
Bonne journée

e^{-x}.e^{-x} = e^{-x-x}= e^{- 2x} Ok mais dans l'exo c'est pas une multiplication mais une addition oui, je sais ! Je vais t'écrire proprement le développement : http://img1.imagilive.com/0117/130.JPG . . . où alors, il y a quelque chose qui m'a échappé . . . ! ? . . . Merci c'est gentil mais je p...

laetidom a écrit:

Ok mais dans l'exo c'est pas une multiplication mais une addition

J'ai trouvé ça : J'ai mis la fonction f(x) au carré et idem pour g(x) et j'ai mis un - entre les 2. En essayant de simplifier j'ai trouvé: (e^-x + e^-x - e^-x + e^-x / 2 )² = (1+1-1+1 / 2)² = (2/2)² = 1 C'est bon ? Tu as surement bon, mais pour l'instant j'essaye de retrouver . . .( ( e^-x + e^-x -...

Exo 1 : 1-Simplifier les expressions suivantes pour x réel quelconque. b) (e^-2x) * (e^-x)² J'ai trouvé ça: e^-4x ok ! c) e^x-1 / e^x+2 J'ai trouvé ça : e plutôt e^-3 C'est bon ? http://img1.imagilive.com/0117/12923d.JPG D'accord merci pour l'exo 1 q°1 mais pour l'exo 1 q°2 J'ai essayer de faire la...

Bonjour Laaure, Bonjour. Ah d'accord ok j'ai compris ! Merci. quote] S U P E R B E ! Et pour l'exercice 1 question 2 qlq'un à compris svp ?[/ Je regarde ! Peux-tu mettre les parenthèses aux bons endroits de f(x) et g(x) car je ne suis pas devin, merci d'avance ! Ok merci. Dans la question les paren...

Bonjour, Au collège ? Je n'ai jamais vu les fonctions exponentielle au collège. Bonjour Laaure, Ce que l'on voulait te faire remarquer, c'est que : a^x.a^y = a^{x+y} exemple : x^3.x^2 = x^{3+2} = x^5 donc e^2.e^{-x} = e^{2+ (-x)} = e^{2 - x} Comprends-tu ? Bonne journée. Bonjour. Ah d'accor...

Tu es sûr que c'est une fois et pas un plus car dans mon cahier de cours j'ai marqué que e^x + e^y = e^x+y et non pas e^x*y ? salut et qu'as-tu fait au collège ? n'y as-tu pas appris les règles sur les exposants ? Bonjour, Au collège ? Je n'ai jamais vu les fonctions exponentielle au collège.

Tu es sûr que c'est une fois et pas un plus car dans mon cahier de cours j'ai marqué que e^x + e^y = e^x+y et non pas e^x*y ?

laetidom a écrit:Bonjour,

Laaure02 a écrit:
Exo 1 :
1-Simplifier les expressions suivantes pour x réel quelconque.
a) e²*e^-x J'ai trouvé ça : e^2.1/e^x donc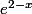

D'accord merci du coup e² * e^-x = e^2*1/e^x = e ^2-x C'est ça ?

Bonjour, J'ai un DM à rendre sur les fonctions exponentielles mais il y a certains exercices où je n'y arrive pas. Pourriez-vous m'aider ? Exo 1 : 1-Simplifier les expressions suivantes pour x réel quelconque. a) e²*e^-x J'ai trouvé ça : e^2+1/e^x b) (e^-2x) * (e^-x)² J'ai trouvé ça: e^-4x c) e^x-1 ...

Bonsoir, Tu apprends.... Oui c'est ça, A² est la matrice inverse de A², c'est-à-dire d'elle-même, car A² * A² = I. Imagine-toi regardant vers le Nord. La matrice A correspond à faire 1/4 de tour dans le sens des aiguilles d'une montre. A^-1 correspond à faire 1/4 de tour dans l'autre sens. Tu peux ...

Pseuda a écrit:Toujours pas.

Une indication : A^2 * A^2 = I

Décidément... Je ne suis pas douée !

A² ? C'est possible ?

Pseuda a écrit:Exact. On a : A^3 * A = A^2 * A^2 = A^4 = I

Tu te rends compte que tout ça, c'est parce que A^4 = I, et qu'on peut décomposer le A^4 comme on veut : A^4 = A^3 * A = A^2 * A^2 = A * A^3 ?

Conclusion : quelle est la matrice inverse de la matrice A^2 ?

Ok donc la matrice inverse de A² c'est A⁴ ?

Pseuda a écrit:A^3 * A ^2 = A ^ ? = A

Donc cela ne fait pas I.

A^3 * A^2 I, donc A^3 n'est pas l'inverse de la matrice A^2.

A^3 *A²=A^5=A

C'est A^3 * A qui est égal à I Soit A²*A² ou A^4

Pseuda a écrit:Celle que tu as écrit, c'est

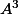
Or A^3 * A^2, cela fait quoi ?

A^3 * A²=
(-2 3 -5
0 1 0
1 -1 2)

C'est à dire A .

Donc A serait l'inverse de la matrice A² . C'est ça ?

Pseuda a écrit:Exact ! C'est-à-dire les 2 matrices sont l'inverse l'une de l'autre.

Comme les nombres 3 et 1/3 sont l'inverse l'un de l'autre (car 3 * 1/3 = 1/3 * 3 = 1).

D'accord du coup l'inverse de la matrice A² c'est
(2 -1 5
0 1 0
-1 1 -2)

C'est ça ?