DM matrices inverse Terminale Es

[Laaure02]

Bonjour,

J'ai un DM a faire pendant les vacances cependant, je bug sur un exercice. Pourriez-vous m'aidez svp ?!

L'exercice est le suivant:

Soit la matrice A=(-2 3 -5
0 1 0
1 -1 2).
1-Avec la calculatrice, calculer les matrices A², A^3 et A^4.

→Donc j'ai trouvé :
A²=( -1 2 0
0 1 0
0 0 -1)

A^3= (2 -1 5
0 1 0
-1 1 -2)

A^4= (1 0 0
0 1 0
0 0 1)

2-En déduire que A est inversible et déterminer A^-1.

→Et là je bug, dans mon cours il y a que la méthode avec des matrices de format (2;2). Il faut bien sûr le faire à "la main" et non pas à la calculatrice !

3-Déduire de la question 1 que A² est inversible et déterminer sa matrice inverse.

→ Du coup, là c'est pareil je n'y arrive pas.....


Voilà ! J'espère que vous pourrez m'aider, merci d'avance à ceux qui le feront.

[Manny06]

Il suffit que tu trouves une matrice M telle que A*M=M*A=I

or tu sais que A^4 =I donc A*.....=I complète


ensuite tu remarqueras que A^4 peut se décomposer de deux façons en produit de 2 matrices......

[Laaure02]

Il suffit que tu trouves une matrice M telle que A*M=M*A=I

or tu sais que A^4 =I donc A*.....=I complète


ensuite tu remarqueras que A^4 peut se décomposer de deux façons en produit de 2 matrices......

Merci pour ta réponse!
Donc si j'ai bien compris A^-1=A*A^4 C'est ça ?
Donc la matrice inverse serait:
A^-1 = (-2 3 -5
0 1 0
1 -1 2)

Mais quand j'entre la matrice A dans ma calculatrice j'obtiens pas le résultat. La calculatrice me donne:
A^-1= (2 -1 5
0 1 0
-1 1 -2)


Et A^4 = A²*A² ?

PS: désolé pour toutes ces questions mais j'ai du mal à comprendre.... :

[Pseuda]

Donc si j'ai bien compris A^-1=A*A^4 C'est ça ?

Bonsoir,

En effet ce n'est pas ça. A^4 = I, et il faut trouver une matrice M telle que A * M = I.

Tu as ainsi tous les éléments pour trouver la solution. Bon, un indice quand même : décomposer A^4 en A * ?

[Laaure02]

Donc si j'ai bien compris A^-1=A*A^4 C'est ça ?

Bonsoir,

En effet ce n'est pas ça. A^4 = I, et il faut trouver une matrice M telle que A * M = I.

Tu as ainsi tous les éléments pour trouver la solution. Bon, un indice quand même : décomposer A^4 en A * ?

Bonjour,
Je suis vraiment désolé j'ai du mal à comprendre !
A^4 je peux le décomposer en A²*A² non ?

[Pseuda]

Bonjour,

Il y a d'autres décompositions de : .

[Laaure02]

Bonjour,

Il y a d'autres décompositions de : .

D'accord donc si par exemple je fais A^3*A, j'obtient (1 0 0
0 1 0
0 0 1)
C'est à dire A^4 mais je peux en déduire A^-1 si ?

[Pseuda]

donc , donc comme on sait que l'inverse d'une matrice, si elle existe, est unique, quelle est la matrice telle que ?

[Laaure02]

donc , donc comme on sait que l'inverse d'une matrice, si elle existe, est unique, quelle est la matrice telle que ?

Ah je crois que je viens de comprendre, La matrice M est A^3 ?!
Car A^3*A=A*A^3=I
C'est ça ?

[Pseuda]

Oui, c'est ça.

[Laaure02]

Oui, c'est ça.

D'accord merci .
Du coup là on en déduit que A est inversible.
Je vais encore t’embêter un peu (désolé). Comment trouve t-on A^-1 stp ?

[Pseuda]

Oui, on en déduit du coup que A est inversible car il existe une matrice M telle que M * A = A * M = I, et cette matrice M, quelle est-elle ? C'est celle qui vérifie cette relation, et pas une autre, c'est laquelle ?

Rappel de l'inverse d'une matrice : c'est LA matrice M telle que M * A = A * M = I

Le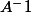 est juste une notation pour désigner l'inverse d'une matrice, mais ce n'est pas là ce qui permet de la trouver.

[Laaure02]

Oui, on en déduit du coup que A est inversible car il existe une matrice M telle que M * A = A * M = I, et cette matrice M, quelle est-elle ? C'est celle qui vérifie cette relation, et pas une autre, c'est laquelle ?

Rappel de l'inverse d'une matrice : c'est LA matrice M telle que M * A = A * M = I

La matrice M c'est A^3 non ? C'est à dire
(2 -1 5
0 1 0
-1 1 2)

Ah du coup A^-1 serait égale à A^3 ?

[Pseuda]

C'est bien ça. Tu peux vérifier avec ta calculatrice.

[Laaure02]

C'est bien ça. Tu peux vérifier avec ta calculatrice.

D'accord merci beaucoup !
Bonne journée.

[Laaure02]

Désolé mais du coup pour la 3eme question A² n'est pas inversible ?

[Pseuda]

Bonjour,

Si 2 matrices A et B sont telles que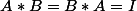 , que peux-tu dire de A et B ?

Ici, que fait ?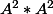

[Laaure02]

Bonjour,

Si 2 matrices A et B sont telles que , que peux-tu dire de A et B ?

Ici, que fait ?

Alors on peut dire que la matrice est inversible mais c'est quoi la matrice B ?

A² *A²=
(1 0 0
0 1 0
0 0 1).

[Pseuda]

La matrice B est du coup l'inverse de la matrice A. Comme la matrice A est l'inverse de la matrice B.

Donc c'est quoi dans ton exercice l'inverse de A² ?

[Laaure02]

La matrice B est du coup l'inverse de la matrice A. Comme la matrice A est l'inverse de la matrice B.

Donc c'est quoi dans ton exercice l'inverse de A² ?

J'ai pas trop compris ....
En gros B=A^-1 ? et A=B^-1 ?