Forum de Mathématiques: Maths-Forum

Bonsoir, voici le problème : On se propose de comparer la fiabilité de deux types d'avions : un biréacteur et un quadriréacteur. On note p la probabilité de panne d'un réacteur quelconque au cours d'un vol quelconque. On suppose que les réacteurs fonctionnent de manière indépendante. De plus, un avi...

Bonjour, Pour le c et le d il faut tracer le tableau de variation de f, en déduire le signe de f' puis tracer une courbe (parmi toutes celles possibles) qui respecte ce signe. C'est à dire si f' est positive sur un intervalle I, la courbe la représentant sur I est située au dessus de l'axe des absc...

Bonsoir, voici l'énoncé : Soit f une fonction définie sur l'intervalle [-1 ; 5] donc la représentation graphique est donnée. Dans chaque cas, donner l'allure approximative de la courbe représentative de la fonction f', dérivée de la fonction f sur l'intervalle [-1 ; 5]. https://www.ilemaths.net/img/...

Ah j'ai trouvé, c=0 et b=0 f(x)=ax² f(4)=2 a*4²=2 16a=2 a=1/8 Et ça passe sur géogébra. Maintenant, pour P2: -tangente g'(4) = 1 4a+b=1 -B(8,0) g(8) = 0 64a+8b+c=0 -I(4,2) g(4) = 2 16a+4b+c=2 J'ai mes 3 dernières équations , j'ai aucune idée de comment faire pour trouver a,b et c d'un coup...

Oui, la courbe passe par (4;4) au lieu de passer par (4;2)...

En testant plusieurs possibilités j'ai vu que 1/8x² passait par (4;2), si ça peut aider...

Et donc, si vous confirmez que c'est correct, b=c=0


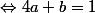
Eeeeeeeeeeeeeeeet doooonc : f(x)=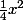
Ca m'a l'air beaucoup trop facile, j'ai l'impression d'avoir foiré qq part

Puis,

Lostounet a écrit:f'(0) vaut aussi 0 (vu qu'en A la parabole est tangente à l'axe des abscisses, cela signifie qu'au point 0, la pente de la tangente est nulle)

Donc b=0 ?

Je pense avoir légèrement avancé mais à partir de là je sais plus où aller : POUR P1 D'abord, Tu peux commencer par traduire l'appartenance de I à la première parabole f(4)=2 Soit 4a^{2}+4b+c=2 Puis, La courbe C ci-dessous est formée de deux arcs de parabole qui se raccordent au point I. La ...

En voulant faire court j'ai oublié les bonnes manières
Bonjour et merci à tous,
POUR P1 [0,4]
.ax²+bx+c=0
.a*4²+b*4+c=2
4a²+4b+c=2
.2a+b=1 ou ax+b=0
POUR P2 [4,8]
.8a²+8b+c=0
.4a²+4b+c=2
.4a+b=1
Et à partir de là je fais comment?

La courbe C ci-dessous est formée de deux arcs de parabole qui se raccordent au point I. La courbe C est tangente à l'axe des abscisses au point A et, pour que le raccordement entre les deux arcs de parabole soit bien "lisse" les pentes des deux demi-tangentes au point I sont égales à 1. ...

Il y a eu un éclair dans ma tête...
Coef dir: yb-ya/xb-xa = -0.1461
Ordonnée à l'origine : 310
Y(x)=-0.1461x+310
Merci infiniment c'est une aide énorme..
Sur ce, bonne nuit
EDIT: je fais la même chose de l'autre côté

Je sèche là..
peut etre yb-ya/xb-xa?
si c'est ça j'essaie de faire ça vite sinon je vais dormir, j'ai du mal à rester debout là

Oui bien sûr, je voulais vous épargner ça.
A partir du moment que j'ai b1... b2 c'est du gâteau
b2= -Ra(8/375)/-2/1875
b2=136.9306394

<=>0=b²/1875 -10
Δ=-4*1/1875*-10
Δ=8/375
b1=Ra(8/375)/-2/1875
b1=-136.93

Ca me semble correct

T:0=-2b²/1875+b²/1875+300
0=-b²/1875+300
Δ=-4*-1/1875*300
Δ=16/25
b1=Ra(16/25)/-2/1875
b1=-750
Je m'étais trompé mais je suis toujours loin des 150...

Bah déjà, à l'issue de cette équation j'obtiens un polynôme... Qui devrait correspondre aux deux points b1 et b2 de ma parabole. Sauf, que d'après géogébra, ça devrait correspondre à -150 et 150..
D'après ce calcul, j'obtiens 32475.95264
On a du oublier un truc quelque part...

Ce qui nous donne :
f(b)=-2b/1875
T: y=(-2b/1875)*(x-b)+f(b)
T:310=(-2b/1875)(0-b)-b²/1875+300
?

+2b?
Il me semble avoir déjà vu des 1/x = -1/x² mais pas de 1/k... J'aimerai bien être (encore) éclairé sur ce coup-ci :S

D'accord donc si j'ai bien compris: (j'utilise b à la place de a, qui est déjà utilisé dans mon devoir) T: y=-2b(x-b)+f(b) T:310=-2b(0-b)-b²/1875+300 Je continue sur cette voie là, et donc j'obtiens un polynome qui me donnera les points de contact tangente/parabole des deux cotés si j'ai bien tout c...

Si je continue,
Δ=0²-4*(3751b²/1875)*(-610)
Δ=4881.301333

Donc, b1= Racine(4881.301333)/-7502/1875
b1= -17.4619211
et b2=17.4619211

Cependant.. ça colle pas du tout avec la représentation géogébra que j'ai faite... je devrai trouver 150