Forum de Mathématiques: Maths-Forum

Merci sujet résolu, merci encore mrif :we:

Ce que tu as écrit est vague et je ne vois pas l'intérêt de l'introduction de la variable aléatoire Z. Quelle est la densité de la variable aléatoire (X,Y)? Comment caractériser le domaine D = {Y<1-X} ? Que signifie P(Y<1-X) ? Si f est la densité du couple (X,Y) aors P(Y<1-X) est l'...

mrif a écrit:Fais un dessin en traçant la droite d'équation X+Y=1 et repère le domaine qui convient.

Ok donc si X et Y sont indépendantes, alors Z=1-X et que X et Z sont indépendantes, alors:

(car symétrique), c'est bien ça la reponse ?

Bonjour,

Si deux variables X et Y suit une loi uniforme [0,1]
Alors si par exemple on veut essayer de calculé la probabilité que P[X²+Y²<=1]
la réponse est Aire du cercle /Aire du carrée =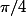 . Mais si on essaye de calculer la probabilité que P[X<1-X] ou P[Y<1-X] comment fait-on ?

Sinon je pensait plutôt à calculer f(x+h), d'où:

est notre dérivée si A est symétrique, qu'en pensez vous ?

Que vaut le gradient de f: R^n->R telle que f(x)=x^{T}*Ax ou À est une matrice carrée de taille n*n non symétrique ? Et si A est symétrique que vaut le gradient ? Moi je pensait déjà que si A est symétrique alors : \nabla y = x^{T}(A+A^{T}) dy = dx^{T}Ax + x^{T}Adx = x^{T}(A+A^{T...

Bonjour, J'ai essayé de faire quelques exercices sur l'optimisation sous contrainte avec le lagrangien mais je sais pas si déjà les quelques réponses sont justes et comment résoudre les autres questions que je n'arrive pas à résoudre, merci. :we: :we: :we: http://www.casimages.com/i/1510011003466525...