Probabilité de la loi uniforme

[stroke599]

Bonjour,

Si deux variables X et Y suit une loi uniforme [0,1]
Alors si par exemple on veut essayer de calculé la probabilité que P[X²+Y²<=1]
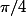
la réponse est Aire du cercle /Aire du carrée = . Mais si on essaye de calculer la probabilité que P[X<1-X] ou P[Y<1-X] comment fait-on ?

[mrif]

Fais un dessin en traçant la droite d'équation X+Y=1 et repère le domaine qui convient.

[stroke599]

Fais un dessin en traçant la droite d'équation X+Y=1 et repère le domaine qui convient.

Ok donc si X et Y sont indépendantes, alors Z=1-X et que X et Z sont indépendantes, alors:

(car symétrique), c'est bien ça la reponse ?

[mrif]

Ce que tu as écrit est vague et je ne vois pas l'intérêt de l'introduction de la variable aléatoire Z.

Quelle est la densité de la variable aléatoire (X,Y)?
Comment caractériser le domaine D = {Y<1-X} ?
Que signifie P(Y<1-X) ?

Si est la densité du couple aors est l'intégrale sur de ,
où si (x,y) appartient à et 0 sinon.

Tu trouveras:

et est le triangle (plein) rectangle et isocèle de sommets (0;0), (1,0) et (0,1).
Le résultat de l'intégration est 1/2.

Bon courage

[stroke599]

Ce que tu as écrit est vague et je ne vois pas l'intérêt de l'introduction de la variable aléatoire Z.

Quelle est la densité de la variable aléatoire (X,Y)?
Comment caractériser le domaine D = {Y<1-X} ?
Que signifie P(Y<1-X) ?

Si est la densité du couple aors est l'intégrale sur de ,
où si (x,y) appartient à et 0 sinon.

Tu trouveras:

et est le triangle (plein) rectangle et isocèle de sommets (0;0), (1,0) et (0,1).
Le résultat de l'intégration est 1/2.

Bon courage

Merci sujet résolu, merci encore mrif

[stroke599]

Merci sujet résolu, merci encore mrif :we: