Forum de Mathématiques: Maths-Forum

D'accord, merci beaucoup !

D'accord, donc on arrive à ce qui équivaut à , mais après je ne vois pas comment continuer...

Merci !
Mais pourquoi ?
J'aurai plutôt dit

Bonjour, pourriez-vous m'aider à montrer que si alors , s'il vous plaît ?
Merci d'avance

D'accord, merci beaucoup !

D'accord, merci beaucoup, j'ai peut-être compris !
Donc en gros pour résumer, comme et 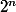ne congruent pas vers le même nombre modulo 4, ça signifie que l'équation n'a pas de solution ?

Et en quoi le fait que et , implique que n'a pas de solution, s'il vous plaît ?

D'accord, merci beaucoup !

D'accord, merci, mais pourquoi 4k²+4k+1=1 mod 4 ?

D'accord, merci beaucoup, j'ai compris ! Est-ce que vous pourriez également m'aider à prouver que , avec 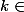. Merci !

Bonjour, pourriez-vous m'aider à prouver que si 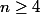, , s'il vous plaît ?
Merci d'avance

D'accord, merci beaucoup !

D'accord, donc les valeurs de l'entier naturel n pour lesquelles est divisible par 15 sont 4k-1, 4k, 4k+1 et 4k+2 ?

D'accord, donc les valeurs de n sont 4k, mais y'en a-t-il d'autres ?

Merci de m'avoir répondu, mais ce qui me gêne c'est le -1 dans .

Bonjour, dans un exercice, on me demande de déterminer les valeurs de l'entier naturel n pour lesquelles 67^{n}-1 est divisible par 15. Je sais que les restes de la division euclidienne des puissances de 67 par 15 sont 1 si n = 4k, 7 si n = 4k + 1, 4 si n = 4k + 2 et 13 si n = 4k + 3, avec k \in ;),...

D'accord, merci beaucoup !

Bonjour, je ne comprends pas très bien un exercice et j'aurais besoin d'un peu d'aide, s'il vous plaît. Voici l'énoncé : On suppose que l'écriture décimale d'un entier x est \overline{ab} avec a \ne 0, c'est-à-dire x = 10a + b. On note y l'entier obtenu en intervertissant les chiffres de x. Démontre...

D'accord, merci beaucoup !

D'accord, merci beaucoup, mais comment je fais pour trouver les autres solutions, s'il vous plaît ?