Critère de divisibilité par 11

[toto273]

Bonjour, je ne comprends pas très bien un exercice et j'aurais besoin d'un peu d'aide, s'il vous plaît.

Voici l'énoncé :

On suppose que l'écriture décimale d'un entier x est 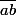avec a 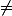0, c'est-à-dire x = 10a + b.
On note y l'entier obtenu en intervertissant les chiffres de x.
Démontrer que x + y est divisible par 11.

J'ai fait :
x = 10a + b
y = 10b + a
x + y = 10a + 10b + a + b
= 11a + 11b
= 11(a + b)

Un entier x comportant quatre chiffres s'écrit dans le système décimal 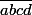avec a 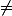0.
En utilisant les congruences modulo 11, démontrer que x 0(11) si, et seulement si :
-a+b-c+d 0(11).

Je ne vois pas comment il faut procéder, pourriez-vous m'aider, s'il vous plaît ?
Merci d'avance

[low geek]

Bonjour,

Si x=
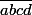
ça veut dire que x=1000a+100b+10c+d
Passe ça en modulo 11 et tu devrais trouver le résultat.

[toto273]

D'accord, merci beaucoup !