112 résultats trouvés
Revenir à la recherche avancée
Donc le 1 est juste!? Pour le 2, je reessaie donc ;) ! Et j'ai essaye le 3 egalement! On considere la suite numerique \left({U}_{n} \right) definie par {U}_{0}=1 et, pour tout entier naturel n , {U}_{n+1}=\frac{1}{3}{U}_{n}+n-1 Soit \left({V}_{n} \right) la suite numerique definie p...
- 05 Sep 2009, 10:46
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 3
- Vues: 751
Re
MERCI Beaucoup de votre aide ! Vous etes trop forts! J'applique ce que vous avez dit! On considère la suite numérique \left({U}_{n} \right) définie par {U}_{0}=1 et, pour tout entier naturel n , {U}_{n+1}=\frac{1}{3}{U}_{n}+n-1 Soit \left({V}_{n} \right) la suite numérique définie po...
- 04 Sep 2009, 23:56
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 3
- Vues: 751
Exercice sur les suites
Bonjour, merci de votre aide sur cet exercice sur les suites! On considère la suite numérique \left({U}_{n} \right) définie par {U}_{0}=1 et, pour tout entier naturel n , {U}_{n+1}=\frac{1}{3}{U}_{n}+n-1 Soit \left({V}_{n} \right) la suite numérique définie pour tout entier n , par {...
- 04 Sep 2009, 22:35
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 3
- Vues: 751
Merci pour votre aide! :) J'ai donc change les choses qui n'allaient pas! Soit ({U}_{n}) une suite definie par : {U}_{n+1} = \frac{3{U}_{n}+4}{{U}_{n}+3} et {U}_{0} = -\frac{3}{2} 1. De quelle facon est definie la suite ({U}_{n}) ? ({U}_{n}) est definie par recurrence 2. Don...
- 02 Mai 2009, 15:25
- Forum: ✎✎ Lycée
- Sujet: [1èreS] Exercice sur les suites
- Réponses: 3
- Vues: 1192
Merci de votre aide! J'avais fait ca avant de revevoir votre message mais je vais aussi essayer ce que vous me conseillez qui est surement beaucoup mieux :P Soit f une fonctions définie sur {\R}^{+} . Soit ({U}_{n}) la suite définie, pour tout n \in \N , par {U}_{n} = f(n) . 1. Montr...
- 02 Mai 2009, 14:14
- Forum: ✎✎ Lycée
- Sujet: [1èreS] Exercice sur les suites
- Réponses: 2
- Vues: 797
[1èreS] Exercice sur les suites
Bonjour d'avance de votre aide sur cet exercice portant sur les suites. Soit ({U}_{n}) une suite définié par : {U}_{n+1} = \frac{3{U}_{n}+4}{{U}_{n}+3} et {U}_{0} = -\frac{3}{2} 1. De quelle façon est définie la suite ({U}_{n}) ? ({U}_{n}) est définie par récurrence. 2. Donn...
- 29 Avr 2009, 19:18
- Forum: ✎✎ Lycée
- Sujet: [1èreS] Exercice sur les suites
- Réponses: 3
- Vues: 1192
[1èreS] Exercice sur les suites
Bonjour d'avance de votre aide sur cet exercice portant sur les suites. Soit f une fonctions définie sur {\R}^{+} . Soit ({U}_{n}) la suite définie, pour tout n \in N , par {U}_{n} = f(n) . 1. Montrer que si f est croissante sur {\R}^{+} , alors la suite ({U}_{n}) est croiss...
- 29 Avr 2009, 18:26
- Forum: ✎✎ Lycée
- Sujet: [1èreS] Exercice sur les suites
- Réponses: 2
- Vues: 797
D'accord :D Merci beaucoup! J'ai un peu reflechi et essaye de faire au propre ce que j'ai pu trouver : {h}_{(A,\frac{2}{5})}(B)=I {h}_{(A,\frac{2}{5})}(C)=J Les droites (IJ) et (BC) sont parallèles. Il existe donc une homothetie h' de centre O qui transforme I en C. S...
- 22 Mar 2009, 15:01
- Forum: ✎✎ Lycée
- Sujet: Exercices sur les homotheties
- Réponses: 5
- Vues: 1451
Merci infiniment de votre reponse!
Dois-je donc d'abord demontrer le parallelisme entre les deux droites?
Mais comment peut-on connaitre ces rapports?
Dois-je donc d'abord demontrer le parallelisme entre les deux droites?
On sait que :
- Deux droites (IC) et (BJ) secantes en A
- I,O,C et J,O,B sont alignes dans le meme ordre
Mais comment peut-on connaitre ces rapports?
- 22 Mar 2009, 11:39
- Forum: ✎✎ Lycée
- Sujet: Exercices sur les homotheties
- Réponses: 5
- Vues: 1451
Exercices sur les homotheties
Bonjour, et merci d'avance de votre aide sur cet exercice sur les homotheties. Soit ABC un triangle. On considere les points I , J et K definis pas : \vec{AI}=\frac{2}{5}\vec{AB} , \vec{AJ}=\frac{2}{5}\vec{AC} , \vec{BK}=\frac{1}{3}\vec{BC} . Les droites (IC) et (BJ) se coupent en un...
- 21 Mar 2009, 00:10
- Forum: ✎✎ Lycée
- Sujet: Exercices sur les homotheties
- Réponses: 5
- Vues: 1451
Exercice sur les produits scalaires
b]Bonjour! Ca serait vraiment gentil de votre part si vous pourriez m'aider tout au long de cet exercice que je n'arrive pas vraiment à faire... Merci beaucoup :) [/b] EFG est un triangle rectangle en E tel que EF=3 et EG=4 1) Construire le barycentre D de (F;4) et (G;3) et le baryce...
- 19 Fév 2009, 18:05
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les produits scalaires
- Réponses: 1
- Vues: 451
premièreExercice : Produit scalaire dans le plan et applicat
Bonjour! Ca serait vraiment gentil de votre part si vous pourriez m'aider tout au long de cet exercice que je n'arrive pas vraiment à faire... Merci beaucoup :) On donne les points A(-3;0) , B(3;-1) et C(1;5) . 1) Déterminer les équations des hauteurs du triangle ABC et en d...
- 19 Fév 2009, 17:25
- Forum: ✎✎ Lycée
- Sujet: premièreExercice : Produit scalaire dans le plan et applicat
- Réponses: 0
- Vues: 777
Exercice sur les limites d'une fonction
Bonjour et merci d'avance de votre aide sur cet exercice. Ce serait super gentil si vous pourriez vérifier l'exercice et m'aider pour les parties que j'arrive pas à faire, MERCI d'avance! La fonction f définie sur \R - \{-1\} par : f(x)=\frac{{x}^{2}+7x+2}{2(x+1)} . On note {C}_{f} ...
- 18 Fév 2009, 22:46
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les limites d'une fonction
- Réponses: 0
- Vues: 740
Je crois qu'il faut calculer la derivee pour la 2b)
 = f(x) - x - 1)
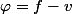
 = x -1)
v'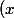= 1)
 '=
'=  '
'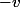 '
'
 '
'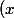) = f'
= f'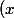 - 1)
La derivee est - elle bonne?
Comment faire pour le minimum...
v'
La derivee est - elle bonne?
Comment faire pour le minimum...
- 25 Jan 2009, 15:24
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les fonctions dérivées
- Réponses: 4
- Vues: 865
Merci de votre aide! Est ce que cela veut dire: On appelera la fonction: {V}_{cylindre}(h) = \pi (R^2 - (\frac{h}{2})^2)h {V}_{cylindre}(h) = \pi h (R - \frac{h}{2})(R + \frac{h}{2}) car R est une constante. Mais je ne comprends toujours pas ce que je...
- 25 Jan 2009, 13:57
- Forum: ✎✎ Lycée
- Sujet: Exercice Premiere S, 1ereS
- Réponses: 5
- Vues: 1188
Merci beaucoup! 1) f(x) = \frac{-7}{\sqrt{2x+1}} 2x+1 > 0 2x > -1 x > \frac{-1}{2} f est derivable sur ]\frac{-1}{2};+ \infty[ f(x)= -7 \times \frac{1}{\sqrt{2x+1}} f = \frac{1}{v} v(x) = \sqrt{2x+1} v'(x) = \frac{2}{2\sqrt{2x+1}} = \frac{1}{\sqrt{2x+1}} f' = \frac{-v"}{v^2} f'(...
- 25 Jan 2009, 13:43
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les fonctions dérivées
- Réponses: 3
- Vues: 708
Merci pour votre aide!
Est ce que cela veut dire que je dois calculer la derivee de quelque chose d'abord?
Est ce que cela veut dire que je dois calculer la derivee de quelque chose d'abord?
- 25 Jan 2009, 02:38
- Forum: ✎✎ Lycée
- Sujet: Exercice Premiere S, 1ereS
- Réponses: 5
- Vues: 1188
Exercice sur les fonctions dérivées
Bonjour et merci d'avance de votre aide sur cet exercice sur les fonction derivees. Determiner l'intervalle (ou la reunion d'intervalles) de \R sur lequel la fonction f est derivable et calculer sa derivee. 1) f(x) = \frac{-7}{\sqrt{2x+1}} 2x+1 > 0 2x > -1 x > \frac{-1}{2} f est derivable su...
- 25 Jan 2009, 02:35
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les fonctions dérivées
- Réponses: 3
- Vues: 708
J'étais en train d'écrire " Je suis désolé je ne comprends pas " mais je crois avoir compris!!! 2) f > 0 sur R f' = f Donc f' > 0 sur R f' > 0 sur R f strictement croissante sur R f' = f Donc f' est strictement croissante sur R. Est ce bon? Pouvez vous m'aidez pour la suite? Je suis désolé...
- 25 Jan 2009, 02:10
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les fonctions dérivées
- Réponses: 4
- Vues: 865
Merci de votre aide! J'ai essayé et ca a donné ca: 1) On appelle le centre de la sphere, O On appelle un point d'intersection inferieur entre le cylindre et le sphere, C On appelle le centre de la base inferieur du cylindre, O'. h qui est la hauteur du cylindre, h est perpendiculaire au rayon r qui ...
- 25 Jan 2009, 01:53
- Forum: ✎✎ Lycée
- Sujet: Exercice Premiere S, 1ereS
- Réponses: 5
- Vues: 1188
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
