Forum de Mathématiques: Maths-Forum

Merci pour votre réponse je reverrai mon programme de 1ere :)

Le programme de spé maths est très spécifique, et n'a pas beaucoup de connexions avec le programme commun. Personnellement, si tu as envie de continuer dans les maths et que est prêt à y consacrer un peu de temps cet été, à ta place, je ferait un peu de logique et je me renseignerait un peu sur les...

zygomatique a écrit:et t'amuser sur des fora de math ...

Des quoi ?

zygomatique a écrit:salut

sans aller à te préparer, du moins réviser à la fin des vacances ce que tu as fait en première ....

Très bien merci

Bonjour, je suis élève en première S et j'ai choisi la spécialité math pour l'année prochaine après hésitation avec la spé physique. J'ai penché pour les maths car mon prof ma dit que le "choc" des heures de maths en prepa serait pris en terminale et je pourrai enchainer l'année post bac sans soucis...

Bonjour,
Pour l'expression de Un j'en arrive donc à Un= V1 * (1-q^n)/(1-q) - Uo mais le résultat n'est pas bon :(

capitaine nuggets a écrit:Je vois pas du tout comment tu trouves ça : on a donc .
Exprime la somme en fonction de et et tu auras ta réponse :+++:

Merci ! Oui je me rend compte que j'ai fait une faute ;)

Merci pour vos réponses précédentes.

Pour ce qui est de l'expression de Un en f° de n, j'en arrive à un résultat incoherant:

Un=Uo*q^n avec Uo=1

ce qui équivaut à Un=q^n mais en cherchant U1 avec cette expression, je ne retrouve pas U1=2 ;)

capitaine nuggets a écrit:Regarde le membre de droite : il va y avoir des compensations :+++:

Ça y est je vois

Re Bonjour,

j'en arrive donc à : V1 + V2 +....+ Vn-1 + Vn = (U1-Uo) + (U2-U1) +....+ (Un-1 - Un-2) + (Un - Un-1)

Dois je soustraire quelque chose ? Ou me servir d'une formule ? Sachant que je dois arriver à Un - Uo

capitaine nuggets a écrit:Re-salut !

Tu peux remarquer que :

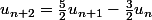
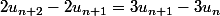
équivaut à équivaut à équivaut à ...

J'ai trouvé la raison! J'ai appliqué sur quelques calculs et ça marche. Merci beaucoup pour votre aide !

Salut ! 1) En partant de l'expression de v_{n+1} , montre qu'il existe un réel q tel que v_{n+1}=q\times v_n . 2) Remarque que v_1+\cdots + v_n=(u_1-u_0)+(u_2-u_1)+(u_3-u_2)+\cdots +(u_{n-1}-u_{n-2})+ ( (u_n-u_{n-1}) :++: 3) v_1+\cdots + v_n est la somme ...

zygomatique a écrit:salut



....

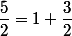
Pourrait tu développer, éclaircir ?

Bonjour j'ai un court dm à faire pour ces vacances et je bloque à certaines questions, notamment: (Un) définie sur N par: -Uo=1 U1=2 et Un+2 = (5/2)Un+1 - (3/2)Un Puis on dit: (Vn) est définie sur N* par Vn=Un-Un-1 1) Montrer que la suite (Vn) est géométrique et en préciser la raison 2) Montrer que ...