DM Suites
17 messages
- Page 1 sur 1
DM Suites
Bonjour j'ai un court dm à faire pour ces vacances et je bloque à certaines questions, notamment:
(Un) définie sur N par:
-Uo=1 U1=2
et Un+2 = (5/2)Un+1 - (3/2)Un
Puis on dit: (Vn) est définie sur N* par Vn=Un-Un-1
1) Montrer que la suite (Vn) est géométrique et en préciser la raison
2) Montrer que V1+V2+...+Vn = Un-Uo
3) En déduire l'expression de (Un) en fonction de n
4) Quel est le sens de variation de (Un) ? Sa limite ?
(Un) définie sur N par:
-Uo=1 U1=2
et Un+2 = (5/2)Un+1 - (3/2)Un
Puis on dit: (Vn) est définie sur N* par Vn=Un-Un-1
1) Montrer que la suite (Vn) est géométrique et en préciser la raison
2) Montrer que V1+V2+...+Vn = Un-Uo
3) En déduire l'expression de (Un) en fonction de n
4) Quel est le sens de variation de (Un) ? Sa limite ?
Salut !
1) En partant de l'expression de , montre qu'il existe un réel
, montre qu'il existe un réel  tel que
tel que  .
.
2) Remarque que+(u_2-u_1)+(u_3-u_2)+\cdots +(u_{n-1}-u_{n-2})+ ( (u_n-u_{n-1})) :++:
:++:
3) est la somme de
est la somme de  termes consécutifs d'une suite géométrique de premier terme
termes consécutifs d'une suite géométrique de premier terme 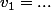 et de raison
et de raison 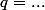 , donc tu as une formule dans ton cours qui te donne directement une expression de
, donc tu as une formule dans ton cours qui te donne directement une expression de  en fonction de
en fonction de  ,
,  et
et  . Déduis-en alors une expression de
. Déduis-en alors une expression de  d'après l'égalité que tu as dû montrer lors de la question précédente.
d'après l'égalité que tu as dû montrer lors de la question précédente.
:+++:
1) En partant de l'expression de
2) Remarque que
3)
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
1) En partant de l'expression de, montre qu'il existe un réel
tel que
.
2) Remarque que:++:
3)est la somme de
termes consécutifs d'une suite géométrique de premier terme
et de raison
, donc tu as une formule dans ton cours qui te donne directement une expression de
en fonction de
,
et
. Déduis-en alors une expression de
d'après l'égalité que tu as dû montrer lors de la question précédente.
:+++:
Salut !
C'est justement ce V (n+1)=q*Vn qui me pose vraiment problème :/
Re-salut !
Tu peux remarquer que :
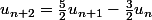 équivaut à
équivaut à  équivaut à
équivaut à 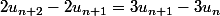 équivaut à ...
équivaut à ...
Tu peux remarquer que :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
biggy34 a écrit:Re Bonjour,
j'en arrive donc à : V1 + V2 +....+ Vn-1 + Vn = (U1-Uo) + (U2-U1) +....+ (Un-1 - Un-2) + (Un - Un-1)
Dois je soustraire quelque chose ? Ou me servir d'une formule ? Sachant que je dois arriver à Un - Uo
Regarde le membre de droite : il va y avoir des compensations :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Je vois pas du tout comment tu trouves ça : on a  donc
donc -u_0) .
.
Exprime la somme en fonction de
en fonction de  et
et  et tu auras ta réponse :+++:
et tu auras ta réponse :+++:
Exprime la somme
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
biggy34 a écrit:Bonjour,
Pour l'expression de Un j'en arrive donc à Un= V1 * (1-q^n)/(1-q) - Uo mais le résultat n'est pas bon
Oui, parce que j'ai oublié de changer un signe lors de l'écriture de mon post :
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
