A bientôt
1110 résultats trouvés
Revenir à la recherche avancée
Re: Intégrale double \sqrt{x^2+y^2 }dxdy
Donc, je propose l'intégrale double.
\:sin (\theta) d(\theta))
A bientôt
A bientôt
- 14 Sep 2024, 17:33
- Forum: ✯✎ Supérieur
- Sujet: Intégrale double \sqrt{x^2+y^2 }dxdy
- Réponses: 14
- Vues: 866
Re: Intégrale double \sqrt{x^2+y^2 }dxdy
Donc on est dans la zone b catamat ?
- 14 Sep 2024, 16:06
- Forum: ✯✎ Supérieur
- Sujet: Intégrale double \sqrt{x^2+y^2 }dxdy
- Réponses: 14
- Vues: 866
Re: Intégrale double \sqrt{x^2+y^2 }dxdy
Donc 
Est-ce que la zone a ressemble à une ellipse ?
Est-ce que la zone a ressemble à une ellipse ?
- 14 Sep 2024, 15:52
- Forum: ✯✎ Supérieur
- Sujet: Intégrale double \sqrt{x^2+y^2 }dxdy
- Réponses: 14
- Vues: 866
- 14 Sep 2024, 15:08
- Forum: ✯✎ Supérieur
- Sujet: Intégrale double \sqrt{x^2+y^2 }dxdy
- Réponses: 14
- Vues: 866
Re: Intégrale double \sqrt{x^2+y^2 }dxdy
Là, je cherche des cours sur les équations cartésiennes des cercles.
A bientôt
A bientôt
- 13 Sep 2024, 23:07
- Forum: ✯✎ Supérieur
- Sujet: Intégrale double \sqrt{x^2+y^2 }dxdy
- Réponses: 14
- Vues: 866
Re: Thermodynamique transformation isochore
Bonsoir
La loi de Charles peut s'écrire sous la forme.

L'expression de en fonction de
en fonction de 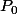 est:
est:

Est-ce que c'est correcte ?
A bientôt
La loi de Charles peut s'écrire sous la forme.
L'expression de
Est-ce que c'est correcte ?
A bientôt
- 13 Sep 2024, 22:16
- Forum: ⚛ Physique
- Sujet: Thermodynamique transformation isochore
- Réponses: 14
- Vues: 2067
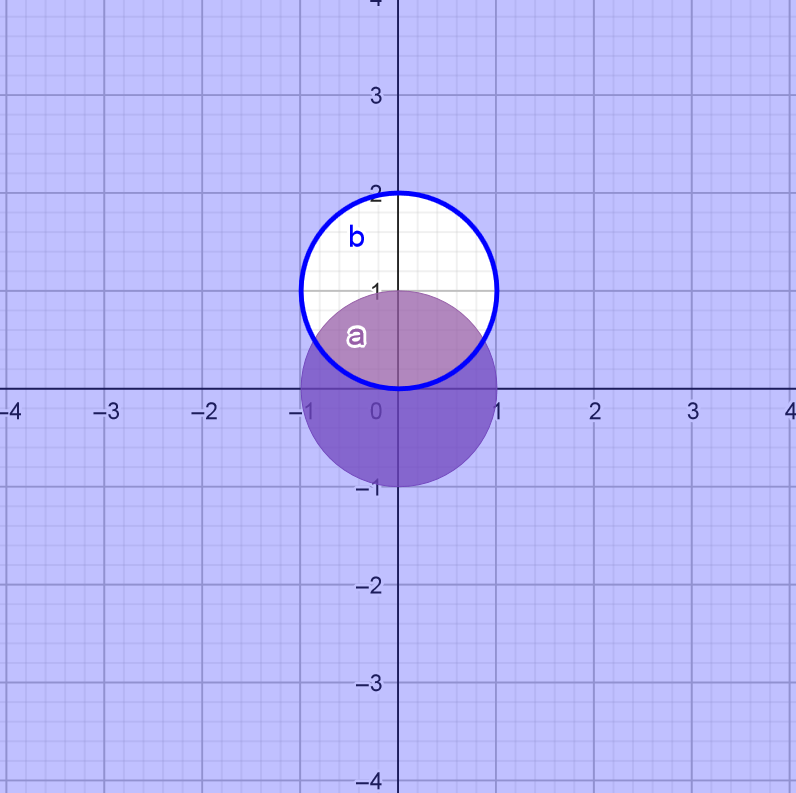
Intégrale double \sqrt{x^2+y^2 }dxdy
Bonsoir Voici une double intégrale. J=\iint_D \sqrt{x^2+y^2 }dxdy où D est le domaine Avec x^2+y^2 \leq 1 et x^2+y^2-2y \geq 0 Pour le moment, je souhaite représenter le domaine D. Est-ce que cela ressemble au dessin ci-dessous, le demi-cercle est D. https://zupimages.net/up/24/37/3vn6.png A bientôt
- 13 Sep 2024, 19:59
- Forum: ✯✎ Supérieur
- Sujet: Intégrale double \sqrt{x^2+y^2 }dxdy
- Réponses: 14
- Vues: 866
Re: Le rotationnel d'un vecteur
Oui, j'ai tapé vite au clavier.
Donc, le résultat est une colonne de trois 0 à la fin ?
A bientôt
Donc, le résultat est une colonne de trois 0 à la fin ?
A bientôt
- 09 Sep 2024, 15:36
- Forum: ✯✎ Supérieur
- Sujet: Le rotationnel d'un vecteur
- Réponses: 3
- Vues: 499
Le rotationnel d'un vecteur
Bonjour On considère le vecteur \vec{V} tel que \vec{V} =x\vec{i} +y \vec{j} + z \vec{k} \vec{rot} \vec{V} = \vec{\nabla} \vec{V} = \begin{pmatrix} \frac{\partial}{\partial x}\\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z} \end{pmatrix} \times \begin{pmatrix} V_x\\ V_y\\ V_z \end{pmatri...
- 09 Sep 2024, 10:46
- Forum: ✯✎ Supérieur
- Sujet: Le rotationnel d'un vecteur
- Réponses: 3
- Vues: 499
Re: Factorisation
Bonjour
Si j'ai bien compris, la factorisation est (x-z)(z-y)(y-x).
A bientôt
Si j'ai bien compris, la factorisation est (x-z)(z-y)(y-x).
A bientôt
- 09 Sep 2024, 10:07
- Forum: ✎✎ Lycée
- Sujet: Factorisation
- Réponses: 3
- Vues: 697
Factorisation
Bonsoir
J’essaie de factoriser
J'ai essayé de commencer par mettre en ordre ci-dessous.
 +x^2(z-y) + y^2(x-z))
Je ne vois pas comment terminer la factorisation.
A bientôt
J’essaie de factoriser
J'ai essayé de commencer par mettre en ordre ci-dessous.
Je ne vois pas comment terminer la factorisation.
A bientôt
- 08 Sep 2024, 21:29
- Forum: ✎✎ Lycée
- Sujet: Factorisation
- Réponses: 3
- Vues: 697
Re: Exercice espace vectoriel
Bonsoir \forall (x,y,z) \in F et \forall (x,'y',z') \in F On n'est bien d'accord que le calcul ci-dessous est faux. (xyz)+ (x'y'z')=0 \Longleftrightarrow (x+x') \times (y+y' ) \times (z+z ') =0 A bientôt
- 20 Mai 2024, 17:56
- Forum: ✯✎ Supérieur
- Sujet: Exercice espace vectoriel
- Réponses: 4
- Vues: 317
Exercice espace vectoriel
Bonjour
On vérifie si F est un espace vectoriel.
 \in \mathbb{R}^3 | xyz = 0\})
Est-ce que \in F)

Il n'est pas possible de vérifier pas addition, F n'est pas un espace vectoriel.
Est-ce que mon raisonnement est correct ?
A bientôt
On vérifie si F est un espace vectoriel.
Est-ce que
Il n'est pas possible de vérifier pas addition, F n'est pas un espace vectoriel.
Est-ce que mon raisonnement est correct ?
A bientôt
- 20 Mai 2024, 08:08
- Forum: ✯✎ Supérieur
- Sujet: Exercice espace vectoriel
- Réponses: 4
- Vues: 317
premier exercice electrostatique
Bonsoir Voici l'exercice. On considère deux charges égales Q positives placées sur un axe Ox en deux points A et B d'abscisses respectives +a et -a. Déterminer la force qui s'exerce sur une charge q placée sur l'axe oy en un point M d'ordonné y positive quelconque. Désolé pour mon schéma, il n'est p...
- 29 Avr 2024, 22:27
- Forum: ⚛ Physique
- Sujet: premier exercice electrostatique
- Réponses: 1
- Vues: 653
Calcul noyau matrice application linéaire
Bonsoir Pourriez-vous s'il vous corriger mes calcul ci-dessous ? Merci ! A = \begin{pmatrix} 2& 7 & 0 &7 \\ 0 &7 &3 &1 \end{pmatrix} f(x, y, z,t) = \begin{pmatrix} 2x& 7 y& 0 &7t \\ 0 &7y &3 z &t \end{pmatrix} Ker(f) = \{(x, y, z,,t...
- 21 Avr 2024, 21:09
- Forum: ✯✎ Supérieur
- Sujet: Calcul noyau matrice application linéaire
- Réponses: 2
- Vues: 267
Déterminer le rang d'une matrice.
Bonjour Est-ce que mon raisonnement ci-dessous est correct ? rang(A)=\begin{pmatrix} 1 &0 &0 &0 \\ 2 & 3 &0 &0 \\ 4 & 5& 6 & 0 \end{pmatrix} = 3 Le rang de la matrice A est 3, car les coefficients de la quatrième colonne sont nuls, il n'y a pas de calcul à...
- 18 Avr 2024, 05:33
- Forum: ✯✎ Supérieur
- Sujet: Déterminer le rang d'une matrice.
- Réponses: 2
- Vues: 308
Re: Algèbre linéaire - application matrice
Bonjour
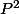 est de degré 2.
est de degré 2.
A bientôt
A bientôt
- 10 Avr 2024, 23:44
- Forum: ✯✎ Supérieur
- Sujet: Algèbre linéaire - application matrice
- Réponses: 6
- Vues: 513
Re: Algèbre linéaire - application matrice
C'est ce qui est noté dans l'exercice.
- 10 Avr 2024, 16:18
- Forum: ✯✎ Supérieur
- Sujet: Algèbre linéaire - application matrice
- Réponses: 6
- Vues: 513
Re: Algèbre linéaire - application matrice
Pardon c'est  \to (P(X))^2)
- 10 Avr 2024, 16:02
- Forum: ✯✎ Supérieur
- Sujet: Algèbre linéaire - application matrice
- Réponses: 6
- Vues: 513
Algèbre linéaire - application matrice
Bonjour Voici un exercice que je souhaite résoudre Soit un entier n \geq 1 Vérifier que les applications suivantes sont des endomorphismes de \mathbb{R}_n [X] , puis déterminer leur matrice dans la base canonique de \mathbb{R}_n [X] f : P(X) \to X P'(X) f : P(X) \to X ...
- 10 Avr 2024, 15:12
- Forum: ✯✎ Supérieur
- Sujet: Algèbre linéaire - application matrice
- Réponses: 6
- Vues: 513
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :