Bonjour,
Je ne comprends pas pourquoi dans le développement du binôme de newton les coefficients binomiaux sont considérés comme des combinaisons de p parmi n et non des arrangements de p parmi n.
Si quelqu'un peut me donner une réponse (assez simple) je le remercie par avance. Bonne journée.
Arrangement et combinaison
Règles du forum
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
4 messages
- Page 1 sur 1
Re: arrangement et combinaison
Bonjour,
Lorsque vous considérez^n) , en développant vous aurez des termes
, en développant vous aurez des termes 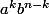 .
.
combien y a-t-il de façon de faire un tel terme :
Mais quand vous "choisissez" ces k facteurs, l'ordre des facteurs est-il important ? Bien sûr que non. Si on a pris les facteurs n° 1, 2, 3, 4 pour avoir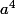 , on ne va pas ensuite prendre les facteurs 2,1,4,3, ni les facteurs 4,3,2,1, etc. ; ce choix (1,2,3,4) est indépendant de l'ordre dans lequel on prend les facteurs.
, on ne va pas ensuite prendre les facteurs 2,1,4,3, ni les facteurs 4,3,2,1, etc. ; ce choix (1,2,3,4) est indépendant de l'ordre dans lequel on prend les facteurs.
On compte donc bien le nombre de "k-facteurs" sans considérer l'ordre de choix, ce qui est bien un nombre de combinaisons et pas un nombre d'arrangements.
Lorsque vous considérez
combien y a-t-il de façon de faire un tel terme :
- pour une occurrence de ce terme, on "choisit" k facteurs dans lequel on ne prend que le a
- et on prend le b dans les (n-k) autres facteurs
Mais quand vous "choisissez" ces k facteurs, l'ordre des facteurs est-il important ? Bien sûr que non. Si on a pris les facteurs n° 1, 2, 3, 4 pour avoir
On compte donc bien le nombre de "k-facteurs" sans considérer l'ordre de choix, ce qui est bien un nombre de combinaisons et pas un nombre d'arrangements.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: arrangement et combinaison
(*) choix d'un indice pour y mettre le "b": 1,2,3. nombre de choix
(**) choix de deux indices pour y mettre "b": {1;2},{1;3} ,{2;3}. nombre de choix
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
