Limite de suite

par **tinkerbell64** » 18 Nov 2013, 18:24

Bonsoir,

je ne comprend pas comment trouver la limite d'une suite lorsqu'on pose lim un = L.
Dans mon exercice, je trouve que lim un est donc égale à 1.4L-0.05L² cependant à partir de la je ne sais pas comment en déduire la limite.. ?

Un exemple dans mon cours dit : u(n+1) = 1/3un+2 donc lim un = 1/3L+2 donc L=3 mais comment trouve-t-on 3?

Merci d'avance pour vos réponses.

par **Carpate** » 18 Nov 2013, 18:49

tinkerbell64 a écrit:Bonsoir,

je ne comprend pas comment trouver la limite d'une suite lorsqu'on pose lim un = L.
Dans mon exercice, je trouve que lim un est donc égale à 1.4L-0.05L² cependant à partir de la je ne sais pas comment en déduire la limite.. ?

Un exemple dans mon cours dit : u(n+1) = 1/3un+2 donc lim un = 1/3L+2 donc L=3 mais comment trouve-t-on 3?

Merci d'avance pour vos réponses.

Peux-tu donner l'expression de

?

par **tinkerbell64** » 18 Nov 2013, 19:00

Carpate a écrit:Peux-tu donner l'expression de ?

J'ai l'expression de u(n+1)=1.4un-0.05un² mais pas celle de un.

par **Carpate** » 18 Nov 2013, 19:06

tinkerbell64 a écrit:J'ai l'expression de u(n+1)=1.4un-0.05un² mais pas celle de un.

Et

?
as-tu montré la convergence de

?

par **tinkerbell64** » 18 Nov 2013, 19:13

Carpate a écrit:Et?
as-tu montré la convergence de ?

u0= 2 et oui, elle converge vers 8, et est minorée par 0.

par **Carpate** » 18 Nov 2013, 19:39

tinkerbell64 a écrit:u0= 2 et oui, elle converge vers 8, et est minorée par 0.

Suite décroissante et minorée admet une limite l
Puisque la fonction

est continue, quand,

,

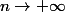
et

donc, au passage à la imite

par **Carpate** » 18 Nov 2013, 19:44

tinkerbell64 a écrit:u0= 2 et oui, elle converge vers 8, et est minorée par 0.

n'est pas décroissante ?

par **tinkerbell64** » 18 Nov 2013, 19:59

Carpate a écrit: n'est pas décroissante ?

non, on a démontrer par récurrence que 0<un<u(n+1)<8

par **Carpate** » 18 Nov 2013, 20:04

tinkerbell64 a écrit:non, on a démontrer par récurrence que 0<un<u(n+1)<8

est continue sur R, donc quand

,

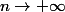
et

et on a donc :

donc les racines sont 0 et 8
Seule l= 8 convient

par **tinkerbell64** » 18 Nov 2013, 20:44

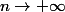
Carpate a écrit: est continue sur R, donc quand , et et on a donc :
donc les racines sont 0 et 8
Seule l= 8 convient

ahhhh d'accord merci bcp!!!! je n'avais pas compris qu'il fallait faire avec les racines du polynôme....... :doh:

Limite de suite

limite de suite

Qui est en ligne