égalité triangulaire complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bichou90
- Messages: 6
- Enregistré le: 04 Nov 2013, 16:10
-
 par bichou90 » 04 Nov 2013, 16:14
par bichou90 » 04 Nov 2013, 16:14
Salut Tout le monde, pourriez vous m'aider à resoudre cette question ?
Repondre par vrai/faux en justifiant :
Mq si |z+z'| = |z|+|z'| alors arg(z)=arg(z')[2pi] z et z' complexes non nuls.
merci d'avance.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Nov 2013, 16:17
par leon1789 » 04 Nov 2013, 16:17
Géométriquement, comment interprètes-tu le module d'un nombre complexe ?
-
bichou90
- Messages: 6
- Enregistré le: 04 Nov 2013, 16:10
-
 par bichou90 » 04 Nov 2013, 16:27
par bichou90 » 04 Nov 2013, 16:27
rayon d'un cercle

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Nov 2013, 16:33
par leon1789 » 04 Nov 2013, 16:33
oui, mais disons plus simplement que |a-b| est la distance entre les points d'affixes a et b.
Ainsi, comment s'interprète géométriquement
|z| = |z - 0| ?
|z'| = |z'+z - z| ?
|z+z'| = |z+z' - 0| ?
...en parlant du triangle formé par les 3 points d'affixes 0, z, z+z'
-
bichou90
- Messages: 6
- Enregistré le: 04 Nov 2013, 16:10
-
 par bichou90 » 04 Nov 2013, 16:53
par bichou90 » 04 Nov 2013, 16:53
ça la distance mais est ce que cette distance si elle est vrai|z+z'|= |z| + |z'| conserve-t-elle l'egalité de deux angles ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Nov 2013, 16:55
par leon1789 » 04 Nov 2013, 16:55
bichou90 a écrit:ça la distance mais est ce que cette distance si elle est vrai|z+z'|= |z| + |z'| conserve-t-elle l'egalité de deux angles ?
oui, j'ai bien compris ton exercice. Mais ce qu'il faut,
c'est que tu comprennes pourquoi on a >.
D'où mes questions sur les modules !
-
bichou90
- Messages: 6
- Enregistré le: 04 Nov 2013, 16:10
-
 par bichou90 » 04 Nov 2013, 17:09
par bichou90 » 04 Nov 2013, 17:09
c'est ça ce que j'ai compris comment on a relié les modules à les arguments

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Nov 2013, 17:21
par leon1789 » 04 Nov 2013, 17:21
bichou90 a écrit:c'est ça ce que j'ai compris comment on a relié les modules à les arguments
pas très français tout ça...
arg(z)=arg(z')[2pi] signifie que 0, z, z' sont alignés, avec z sur le [0, z'], ou z' sur le [0, z].
Donc maintenant, tu veux bien répondre à mes questions ou pas ?
-
bichou90
- Messages: 6
- Enregistré le: 04 Nov 2013, 16:10
-
 par bichou90 » 05 Nov 2013, 09:05
par bichou90 » 05 Nov 2013, 09:05
leon1789 a écrit:pas très français tout ça...
arg(z)=arg(z')[2pi] signifie que 0, z, z' sont alignés, avec z sur le [0, z'], ou z' sur le [0, z].
Donc maintenant, tu veux bien répondre à mes questions ou pas ?
D'accord du moment que ça peut resoudre mon problème

 par busard_des_roseaux » 05 Nov 2013, 10:36
par busard_des_roseaux » 05 Nov 2013, 10:36
bonjour,
quelques formules qui peuvent t'être utiles
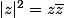
)
=|z| \Leftrightarrow ...)
-
bichou90
- Messages: 6
- Enregistré le: 04 Nov 2013, 16:10
-
 par bichou90 » 07 Nov 2013, 14:25
par bichou90 » 07 Nov 2013, 14:25
Merci beaucoup :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 209 invités
