Trinôme second degrès

[rtva2]

Bonjour ,
J'aurais beoins d'un petit coup de main .Je suis bloqué pour la première question de cet exercice
On pose f(x)=(x²+x-6)(x+1)

1) Expliquez pourquoi le signe de f(x) est celui indiqué dans le tableau ci-dessous.
je n'ai pas compris

------------------------------------------------------------------
x -3 -1 2
------------------------------------------------------------------
x²+x-6 + 0 - - 0 +
------------------------------------------------------------------
x+1 - - 0 + +
----------------------------------------------------------------
f(x) - 0 + 0 - 0 +


2) déduisez de ce tableau l'ensemble des solutions de l'inéquation (x²+x-6)(x+1)<0
Pour cette question j'ai mis que les solutions étaient S: ]-;);-3[ U ]-1;2[
Merci .

[Shew]

Bonjour ,
J'aurais beoins d'un petit coup de main .Je suis bloqué pour la première question de cet exercice
On pose f(x)=(x²+x-6)(x+1)

1) Expliquez pourquoi le signe de f(x) est celui indiqué dans le tableau ci-dessous.
je n'ai pas compris

------------------------------------------------------------------
x -3 -1 2
------------------------------------------------------------------
x²+x-6 + 0 - - 0 +
------------------------------------------------------------------
x+1 - - 0 + +
----------------------------------------------------------------
f(x) - 0 + 0 - 0 +


2) déduisez de ce tableau l'ensemble des solutions de l'inéquation (x²+x-6)(x+1)<0
Pour cette question j'ai mis que les solutions étaient S: ]-;);-3[ U ]-1;2[
Merci .

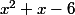
Cherchez les racines de et

[rtva2]

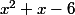
Cherchez les racines de et

Bonjour excuser moi pour le tableau il s'est mal mis l'avez vous compris ?
les racines sont -3 et 2 et -1

[Shew]

Bonjour excuser moi pour le tableau il s'est mal mis l'avez vous compris ?
les racines sont -3 et 2 et -1

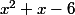
Oui plus ou moin :we: . f(x) est le produit de et de donc si l'un des deux produits est inferieur à 0 alors f(x) < 0 . En raisonnant de façon similaire vous pouvez expliquer le sens des signes du tableau .

[rtva2]

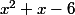
Oui plus ou moin :we: . f(x) est le produit de et de donc si l'un des deux produits est inferieur à 0 alors f(x) < 0 . En raisonnant de façon similaire vous pouvez expliquer le sens des signes du tableau .

justement mon problème ce que je ne vois pas comment expliquer le signe de f(x)

[Shew]

justement mon problème ce que je ne vois pas comment expliquer le signe de f(x)

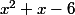
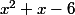
Faisons un essai pour x < -3 , quel sera le signe de x + 1 ? De ? Pourquoi a t'il un tel signe ? Donc quel sera le signe de f(x) ? Pourquoi ?

[rtva2]

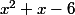
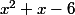
Faisons un essai pour x < -3 , quel sera le signe de x + 1 ? De ? Pourquoi a t'il un tel signe ? Donc quel sera le signe de f(x) ? Pourquoi ?

le signe de x+1 sera positif et le signe de x²+x-6 sera + - + ,le signe et comme cela car a est superieur le signe sera donc positif

[Shew]

le signe de x+1 sera positif et le signe de x²+x-6 sera + - + ,le signe et comme cela car a est superieur le signe sera donc positif

Faux pour x + 1 puisque x + 1 > 0 pour x > -1 donc pour x < -3 , x + 1 ... ?

[rtva2]

Faux pour x + 1 puisque x + 1 > 0 pour x > -1 donc pour x < 3 , x + 1 ... ?

on aura x+1 negatif ?

[Shew]

on aura x+1 negatif ?

-3 ... -1 donc x + 1 ... -3 .

[rtva2]

-3 ... -1 donc x + 1 ... -3 .

-3 -3

[Shew]

-3 -3

Donc quand x < -3, x + 1 .... 0

[rtva2]

Donc quand x < -3, x + 1 .... 0

c'est X+1<0 ?

[Shew]

c'est X+1<0 ?

Et ben oui

[rtva2]

Et ben oui

donc pour expliqué le signe de f(x) je dois dire que puisque x < -3 alors x + 1 < 0 et faire pareille pour les autres ?

[Shew]

donc pour expliqué le signe de f(x) je dois dire que puisque x < -3 alors x + 1 < 0 et faire pareille pour les autres ?

Oui tout en etudiant les signes de .

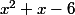
[rtva2]

Oui tout en etudiant les signes de .

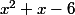
d'accord donc ca ferai puisuqe x 0 ; puisuqe x>2 alors x+1>0 et pour x²+x-6 je fais le meme raisonnement ?

[Shew]

d'accord donc ca ferai puisuqe x 0

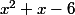
Et puisque ... 0 alors f(x) ... 0 et donc f(x) est ...

puisuqe x>2 alors x+1>0 et pour x²+x-6 je fais le meme raisonnement ?

Comme precedemment .

[rtva2]

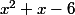
Et puisque ... 0 alors f(x) ... 0 et donc f(x) est ...




Comme precedemment .

x²+x-6>0 alors f(x) <0 donc f(x)est negatif ?

[Shew]

x²+x-6>0 alors f(x) <0 donc f(x)est negatif ?

Voila , faites la même chose pour le reste en vous souvenant que le produit de deux valeurs de signes contraires est toujours négatif .