Ça c'est de la question intéressante ! (Et je vais y réagir en utilisant des notions de terminale S, notamment sur les suites et la convergence. J'espère, Mido123, que tu pourras suivre.)
On construit une suite de chemins (les escaliers) de plus en plus petits qui semblent, à la limite, converger vers la diagonale. Et pourtant leur longueur, elle, ne converge pas vers la longueur de la diagonale !
C'est quoi ce binz ?
Ce problème fait penser aux courbes fractales, qui sont construites un peu comme ces escaliers. Ces courbes sont parfois contre-intuitives, par exemple on peut construite des polygones fractals d'aire finie mais de périmètre infini.
Mais la limite des escaliers, c'est bien la diagonale, n'est-ce pas ?
Précisons un peu les choses... On va définir une suite d'escaliers :
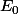
(celui de gauche dans le message de Chan79) qui contient
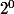
marche de longueur

,

(celui du milieu) qui contient
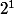
marches de longueur

et ainsi de suite :

contient

marches de longueur
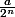
, où

est la longueur d'un côte du carré.
J'ai dit qu'ils convergeaient vers la diagonale. Qu'est-ce que j'entends précisément par là ? Une suite
)
converge vers un nombre

lorsque la valeur absolue de

tend vers 0, c'est-à-dire lorsque la distance de la suite à x (la valeur absolue est une distance) tend vers 0. Converger, c'est une question de distance, donc quand on parle d'un chemin qui converge vers la diagonale, il faut définir une « distance » entre le chemin et la diagonale (ce n'est pas la distance entre deux points, mais la « distance » entre deux courbes).
Je propose de définir
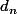
comme étant la distance maximale possible entre un point de

et la diagonale (c'est la définition courante de la « distance » entre deux courbes (*)). Un dessin nous persuade bien vite que la suite des
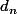
tend vers 0 (on peut montrer facilement qu'elle est par exemple majorée par la suite des
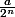
).
Cela signifie donc que la suite des escaliers

converge vers la diagonale (qu'on peut appeler

).
Sauf que leur longueur ne converge pas vers la longueur de la diagonale !
En fait, si on appelle

la fonction qui, à tout chemin, associe sa longueur, on a donc :
- la suite des

converge vers

,
- mais la suite des
)
ne converge pas vers
)
.
Est-ce paradoxal ? Non, ça signifie juste que la fonction

n'est pas continue (**) (seules les fonctions continues ont pour propriété que si la suite des

tend vers

, alors la suite des
)
tend vers
)
, c'est même leur définition).
Donc pour répondre à la question de départ :
comment se fait-il que sous forme d'escalier (même composé d'infimes segments), on obtient une longueur de 2*côtés alors que pour une diagonale parfaite on a une longueur de

2*côté ?
La réponse est :
parce qu'il n'y a pas de raison que ces deux longueurs soient égales. Même si c'est contre-intuitif, ce n'est pas parce que les escaliers tendent vers la diagonale que leur longueur tendra forcément vers celle de la diagonale.
(J'espère n'avoir pas dit trop de bêtises... Mais il me semble que l'essentiel est juste : le paradoxe n'est qu'apparent, il n'y a pas de raison que la limite des escaliers ait la même longueur que la diagonale, même si intuitivement on croit le contraire.)
----
(*) distance = la distance usuelle entre deux points ; « distance » = la distance entre deux courbes telle que je l'ai définie.
(**) plus précisément qu'elle n'est pas continue pour la « distance » choisie - mais là on déborde du programme du lycée.