Trouver deux nombres a et b
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Romane.p59
- Messages: 7
- Enregistré le: 21 Sep 2013, 15:13
-
 par Romane.p59 » 21 Sep 2013, 15:17
par Romane.p59 » 21 Sep 2013, 15:17
Bonjour à tous, je suis en seconde général et j'ai eu un dm de math.
Voici mon dernier exercice que je ne comprend pas :
Trouver deux nombres a et b qui vérifient :(a+b)² # a²+b²
Merci de me répondre au plus vite:)
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Sep 2013, 15:22
par Sourire_banane » 21 Sep 2013, 15:22
Romane.p59 a écrit:Bonjour à tous, je suis en seconde général et j'ai eu un dm de math.
Voici mon dernier exercice que je ne comprend pas :
Trouver deux nombres a et b qui vérifient

a+b)² # a²+b²
Merci de me répondre au plus vite:)
Salut,
Que vaut (a+b)² ?
-
Romane.p59
- Messages: 7
- Enregistré le: 21 Sep 2013, 15:13
-
 par Romane.p59 » 21 Sep 2013, 15:24
par Romane.p59 » 21 Sep 2013, 15:24
Justement je ne sais pas, je pense qu'il faut que je choisie deux nombres au hasard .
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Sep 2013, 15:50
par Sourire_banane » 21 Sep 2013, 15:50
Et moi je te dis que tu peux savoir : Développe (a+b)².
-
Romane.p59
- Messages: 7
- Enregistré le: 21 Sep 2013, 15:13
-
 par Romane.p59 » 21 Sep 2013, 16:07
par Romane.p59 » 21 Sep 2013, 16:07
Moi je crois qu'il faut par exemple a=2 et b=7 pour pouvoir faire (2+7)² # 2²+7² non ?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Sep 2013, 16:12
par Sourire_banane » 21 Sep 2013, 16:12
Non, on veut savoir pour quels nombres a et b on a
^2\not= a^2+b^2)
Il faut donc résoudre une équation.
-
Romane.p59
- Messages: 7
- Enregistré le: 21 Sep 2013, 15:13
-
 par Romane.p59 » 21 Sep 2013, 16:15
par Romane.p59 » 21 Sep 2013, 16:15
Non il y a le signe # donc sa ne peut pas être une équation.
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Sep 2013, 16:19
par Sourire_banane » 21 Sep 2013, 16:19
Traite le cas où c'est égal et déduis-en quand ça ne peut pas être égal.
-
Romane.p59
- Messages: 7
- Enregistré le: 21 Sep 2013, 15:13
-
 par Romane.p59 » 21 Sep 2013, 16:22
par Romane.p59 » 21 Sep 2013, 16:22
Oui mais pourquoi il me dit de trouver un nombre pour a et b ?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Sep 2013, 16:24
par Sourire_banane » 21 Sep 2013, 16:24
T'as pas du tout compris ce qu'on te demande de faire.
On te demande très explicitement de trouver a et b tels que :
^2\not=a^2+b^2)
Il faut donc trouver une condition sur a et b telle que
^2=a^2+b^2)
ne soit pas vérifiée.
PS : Mais vu qu'on te demande juste de trouver deux nombres qui vérifient
^2\not=a^2+b^2)
, oui tu peux prendre 2 et 7...
-
Romane.p59
- Messages: 7
- Enregistré le: 21 Sep 2013, 15:13
-
 par Romane.p59 » 21 Sep 2013, 16:26
par Romane.p59 » 21 Sep 2013, 16:26
Même quand tu m'explique je comprend pas..
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Sep 2013, 16:27
par Sourire_banane » 21 Sep 2013, 16:27
Non non c'est bon j'ai lu de travers. Tu peux te contenter de prendre 2 et 7 et l'équation ne sera en effet pas vérifiée...
Mais bon, c'est si inintéressant !
Sinon pour ta compréhension de l'exo :
On a (a+b)²=a²+2ab+b² et on te demande quand est-ce que ce n'est pas égal à a²+b²
On voit que (a+b)²=a²+2ab+b²=a²+b² ssi 2ab=0 c'est-à-dire lorsque a ou b vaut 0.
Donc on a
^2\not=a^2+b^2)
lorsque
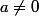
et
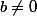
simultanément.
-
Romane.p59
- Messages: 7
- Enregistré le: 21 Sep 2013, 15:13
-
 par Romane.p59 » 21 Sep 2013, 16:32
par Romane.p59 » 21 Sep 2013, 16:32
Ok merci. j'ai compris
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 157 invités
^2\not=a^2+b^2) lorsque
lorsque 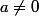 et
et 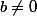 simultanément.
simultanément.