Base de C[X]^n (en tant que C[X]-module)

[professeur plutonium]

Bonjour,

Je suis tombé sur l'exercice suivant :

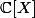
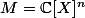
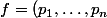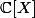
On considère le -module libre et un élément de M tel que . Montrer qu'il existe une base de M (en tant que -module) contenant f.

Mais j'ai du mal... En dimension 2 c'est évident : on regarde la base de M comme une matrice A qui a pour coefficients des polynômes (eux même à coefficient dans C) et det(A)=1 est équivalent au théorème de bezout. (on voit même qu'il y a plusieurs façons de compléter la base) mais dès qu'on passe à n>2 ça pose des problèmes... J'ai essayé par une récurrence sur n, en prenant pour A une matrice circulante ou encore avec de la réduction par opération sur lignes et colonnes mais ça n'a rien donné.

Si quelqu'un a une idée je suis preneur !

[L.A.]

Bonjour.

Le théorème de la base adaptée devrait te sortir d'affaire (C[X] étant heureusement un anneau principal).

[professeur plutonium]

Hum oui c'est sûr ça réglerait le problème mais est ce qu'il n'y aurait pas un moyen détourné de faire ça ? et aussi est ce que le théorème de la base adaptée continu d'être valide si on parle de A-module où A est un anneau non commutatif mais qui dispose quand même d'une division euclidienne ? Parce que j'ai un peu cherché mais à chaque fois que je vois le théorème énoncé c'est toujours dans le cas d'un anneau commutatif...

[L.A.]

Je pense qu'un moyen "détourné" reviendrait toujours plus ou moins à la redémonstration du thm de la base adaptée (c'est vraiment le thm fondamental dans les modules).

Pour le cas non commutatif... je n'en sais rien, tu peux essayer de prendre une démonstration et de voir si elle s'adapte point par point, ou si il y a un truc qui bloque. Sachant qu'il faut faire attention à tout, modules à gauche ou à droite, sans doute division euclidienne à gauche ou à droite, etc...