Minimiser une fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 12 Aoû 2006, 13:42
par tize » 12 Aoû 2006, 13:42
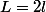
surface toit :

surface sol :

surface mur :

prix en fonction des longueurs :
)
et puisque le volume est :

à reinjecter dans
)
et résoudre l'equation à une inconnue
 par Daragon geoffrey » 14 Aoû 2006, 13:29
par Daragon geoffrey » 14 Aoû 2006, 13:29
slt (petite erreur de vocabulaire de tize) moi je pense quil faut plutôt étudier les variations de la fct f(l)=... sur R pour ainsi déterminer le minimum quelle atteint et trouver le prix le plus bas pour l'édification de la remise ! @ +
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 14 Aoû 2006, 13:33
par tize » 14 Aoû 2006, 13:33
Tout à fait exact Daragon geoffrey, il suffit en effet d'étudier
)
sur
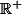

peut s'écrire comme un polynome de degre 3
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 14 Aoû 2006, 14:09
par Sdec25 » 14 Aoû 2006, 14:09
Si on a

,

donc on peut exprimer h en fonction de l et inversement.
Le volume est
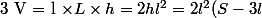<br />= 2 S l^2 - 6l^3)
Il ne reste plus qu'à étudier les variation de cette fonction de l pour trouver un maximum.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 14 Aoû 2006, 14:49
par tize » 14 Aoû 2006, 14:49
Est ce que dans cette question la longueur est toujours le double de la largeur ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 14 Aoû 2006, 19:31
par alben » 14 Aoû 2006, 19:31
Bonsoir,
Ce n'est pas clair : on veut que le volume soit maximal sachant que la somme des trois dimensions doit être constante ?
Le prix n'intervient plus ?
Si c'est le cas, la solution est un classique, c'est un cube. Ca se démontre avec le multiplicateur de Lagrange. On pose L(a,b,h)=abh-k(a+b+h-constante) où a,b et h sont tes 3 dimensions et k le mulplicateur de Lagrange.
On écrit ensuite que les dérivées successives de L par rapport à chaque dimension sont nulles. Du système on sort les valeurs de chaque variable.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 14 Aoû 2006, 19:46
par tize » 14 Aoû 2006, 19:46
je pose x la longueur, y la largeur et z la hauteur avec x+y+z=c (constante)
donc z=c-x-y
on cherche à maximiser le volume : xyz = xy(c-x-y) = x(-y²+y(c-x)).
On fixe x et regarde la formule (-y²+y(c-x)) comme une fonction de y, c'est un polynome de degre 2 a coeff dominant negatif dont les racines sont 0 et (c-x) donc le maximum est atteint pour y=(c-x)/2 et le volume devient alors :
xyz = x(-y²+y(c-x)) <= x( -(c-x)²/4 + (c-x)²/2) en ramplacant y par (c-x)/2
En jolie ça fait :
^2)
Il n'y a plus qu'à trouver le maximum de la fonction
^2)
En dérivant (petite etude de fonction niveau lycee) on trouve que le maximum est atteint pour x=c/3 on en deduit par la suite que c'est bien un cube.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités