Préparer mon ratrappage de maths-info

[nufchavq]

Bonjour
Je passe en 2ème année de prépa d'une école d'ingé (ESILV) et j'ai un ratrappage que je traîne... Bref j'ai commencé à me préparer en général tout va bien mais parfois j'ai mes corrections des TD incomplets du coup je suis pas sur de la rédaction ou du raisonnement Au fur et à mesure de mes révisions je vais certainement poster ici des choses que je ne comprends pas ou que je n'arrive pas à faire et aidez moi si vous avez le temps!! Merci

Voila le premier blème:

Soient A et B deux parties d'un ensemble E, montrer que

• P(A B) = P(A) P(B)

• P(A B) P(A) P(B)

• Donner un exemple où l'égalité entre les deux ensembles du 2ème cas n'est pas vérifiée.

A priori j'ai pas trop de mal avec le maniement des ensembles mais ici je sais pas comment bien démontrer...

Merci de vos propositions!

[nada-top]

bonjour
quelqu'un peut m'expliquer c'est quoi ce P exactement , car je crois qu'il y a une faute dans l'énoncé , sinon je suis complétement perdue :triste:

[Chimomo]

Je supposes que P désigne l'ensemble des parties non ?

Dans ce cas où est ton problème exactement ?

Je supposes que tu as tenté de montrer une double inclusion pour le premier.

[nada-top]

:euh: et moi qui croyais que c'est une simple application de l'ensemble du départ vers l'ensemble d'arrivée car dans ce cas c'est le contraire :
et est inclus dans
je connais cet ensemble des parties mais avec mes outils modestes de première je crois pas que ça va marcher avec cet exo.(mais je vais essayer)

[Chimomo]

Si un élément est dans P(A inter B) alors il s'agit d'un ensemble constitué d'éléments de (A inter B) donc c'est un sous-ensemble de A et un sous-ensemble de B donc il est dans P(A) inter P(B). Si maintenant on prends un élément de P(A) inter P(B), c'est un ensemble constitué d'éléments de A et en même temps un sous ensemble constitué d'éléments de B, donc c'est unsous-ensembles d'éléments de (A inter B). Ainsi il est dans P(A inter B).

On a donc bien P(A inter B) = P(A) inter P(B).

Pour la deuxième partie je te laisse cherche, ainsi que le contre exemple.

[nada-top]

on peut pas démontrer ça par équivalence??
d'ou
c'est ça chimomo ou je me trompe?? :hein:

[Chimomo]

En effet. je voulais éviter le raisonnement par équivalence parceque de façon générale en maths c'est assez "casse-gueule".

C'est pour ça qu'il vaut mieux quand on a une équivalence à montrer faire une double implication, ou une double inclusion dans le cas des ensembles.

Ceci dit sur un exemple qui ne comporte pas dedifficulté ou de piège, on peut en effet raisonner par équivalence.

[nada-top]

pour le contre exemple je crois qu'il suffit de prendre , donc on donc or on a donc
c'est ça ??

[Nightmare]

Il y a un mélange entre les parenthéses et les crochets.

Sans ordre, l'ensemble {0,1} = l'ensemble {1,0} donc P(AUB)={vide,{0},{1},{0,1}}

[mathador]

Salut

Pour la première question, la démonstration de nada-top est excellente, je n'ai rien à ajouter !

pour la deuxième, on peut reprendre l'idée avec des implications :
X appartient à P(A) U P(B) implique X inclu dans A ou dansB, qui implique X inclu dans AUB, d'où la conclusion.


3ème question : A = {1,2} ; B = {3,4} et X = {2,3}. On a bien X est une partie de AUB = {1,2,3,4} ; mais X n'est pas une partie de A, ni une partie de B, donc X n'est pas dans P(A) U P(B)

Voili voilà !
Amicalement

[nada-top]

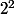
oui exact c'est clair.. doit contenir sous ensembles puisque contient 2 éléments (j'ai rectifié), c'est juste une faute d'inattention et désolée pour le mélange des crochets et parenthèses , j'ai pas arrivé à mettre les crochets de gauche:girl2:
merci nightmare

[nufchavq]

Vous avez été super réactifs merciEffectivement la méthode de la double inclusion c'est celle qui me tentait mais je ne savais pas si c'était vraiment celle qu'on attendait. Bref c'est très clair maintenant merci
Bientôt j'attaquerai les groupes et anneaux et alors là je sens déjà venir une avalanche de questions mdr

[nufchavq]

Rebonjour
Imaginons un énoncé: Soient un ensemble E et deux parties A et B de E, blablabla

Est-ce que ça implique que A et B forment un recouvrement de E ou est-ce qu'il peut y avoir d'autres parties mais dont on ne précise pas l'existence?

Tout ca pour clarifier l'énoncé de ce problème:

Soient un ensemble E et deux parties A et B de E, on considère l'application

f: P(E) ===> P(A)xP(B)
X |==> (X A, X B)

trouver les conditions nécessaires et suffisantes sur A et B pour que l'application f soit:
• injective
• surjective
• bijective

pour le faire il faut que je sois sur s'il y a d'autres parties que A et B dans E, non?

[nada-top]

Hola

je crois pour l'injectivité il faut que ; soient appartenant à
on a alors pour que l'application soit injective donc

[Huit]

Salut,
Pour ce qui est de la surjectivité....

**Si , on choisit :
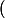
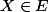
Le couple {} n'a pas d'antécédent. En effet, pour tout , {} d'où . Donc f n'est pas surjective.
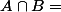
**Si , soient et . On pose et il vient , ainsi . f est donc surjective.

On peut donc conclure que f est surjective ssi

Comme Nada-top la montré, f est injective ssi .

Donc f est bijective ssi et

[nufchavq]

Je dois admettre que c'était pas évident pour moi la surjectivité (à retrouver, pas à comprendre).
Au niveau de l'injectivité je tentais tout le temps avec la contraposée de la définiton (x1 != x2 <=> f(x1) != f(x2), une habitude) du coup j'ai jamais trouvé le bon chemin :(
OK merci pour cet exo
la suite arrive, demain sans doute :))
ca sera dans le dénombrement ou les groupes, je sais pas encore...

[Chimomo]

Une petite récapitulation pour éclairer la notion de recouvrement sur laquelle nufchavq s'est un peu embrouillé :

L'application est injective ssi A et B forment un recouvrement de E.

Elle est surjective ssi ils sont disjoints.

Donc elle est bijective ssi A et B forment une partition de E.