Un exercice non compris!

par **chacchou** » 19 Déc 2012, 16:53

j'ai un exercice d'un devoir maison a faire le problème est que je n'ai pas compris comment le résoudre.
est ce que vous pourriez m'aider à le résoudre le voici:

soit A,B,C 3 point non alignés
Démontrer qu'il n'existe pas de point M vérifiant l'égalité 2MA(vecteur) + MB(vecteur)-3MC(vecteur)=0(vecteur)

merci d'avance (à rendre demain)
vite s'il vous plait!

par **Carpate** » 19 Déc 2012, 17:15

chacchou a écrit:j'ai un exercice d'un devoir maison a faire le problème est que je n'ai pas compris comment le résoudre.
est ce que vous pourriez m'aider à le résoudre le voici:

soit A,B,C 3 point non alignés
Démontrer qu'il n'existe pas de point M vérifiant l'égalité 2MA(vecteur) + MB(vecteur)-3MC(vecteur)=0(vecteur)

merci d'avance (à rendre demain)
vite s'il vous plait!

Démonstration par l'absurde : suppose que le point M existe qui vérifie :

En utilisant la relation de Chasles exprime

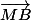
et

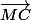
en "passant" par A.
Quelle relation impossible obtiens-tu entre

et

?

par **annick** » 19 Déc 2012, 17:27

Bonjour,
autre façon de démontrer (on suppose qu'il y a des flèches de vecteurs partout) :

2MA+MB-3MC=0

Chasles avec introduction de A :

2MA+(MA+AB)-3(MA+AC)=0
AB-3AC=0
AB=3AC les vecteurs AB et AC sont colinéaires et A,B,C alignés, ce qui est contraire à l'hypothèse de départ.

par **Carpate** » 19 Déc 2012, 17:40

annick a écrit:Bonjour,
autre façon de démontrer (on suppose qu'il y a des flèches de vecteurs partout) :

2MA+MB-3MC=0

Chasles avec introduction de A :

2MA+(MA+AB)-3(MA+AC)=0
AB-3AC=0
AB=3AC les vecteurs AB et AC sont colinéaires et A,B,C alignés, ce qui est contraire à l'hypothèse de départ.

Je ne vois pas en quoi c'est une autre façon de le démontrer

par **annick** » 19 Déc 2012, 18:06

Excuse-moi, Carpate, c'est juste que j'ai vu un peu vite "démonstration par l'absurde" et que je me suis focalisée là-dessus. Désolée.

par **Carpate** » 19 Déc 2012, 18:50

annick a écrit:Excuse-moi, Carpate, c'est juste que j'ai vu un peu vite "démonstration par l'absurde" et que je me suis focalisée là-dessus. Désolée.

Bonsoir, mais ce n'est pas grave (si on pense qu'il ne reste que 2 jours à la terre) !

par **chacchou** » 19 Déc 2012, 20:06

Carpate a écrit:Je ne vois pas en quoi c'est une autre façon de le démontrer

alors est ce que cette solution est elle possible?

par **Carpate** » 19 Déc 2012, 20:11

chacchou a écrit:alors est ce que cette solution est elle possible?

As-tu rencontré déjà des triangles dont les sommets sont alignés ?

par **chacchou** » 19 Déc 2012, 20:17

Carpate a écrit:As-tu rencontré déjà des triangles dont les sommets sont alignés ?

ah non quand meme pas

par **chacchou** » 19 Déc 2012, 20:21

cela veut il dire qu'il n'y a aucune réponse a cet exercice si?
parce que sinon j'ai pas trouvé même après avoir lu et relus vos aides.

par **chacchou** » 19 Déc 2012, 20:34

MB+MC=MA (vecteurs)
mais cela n'est pas la relation de chasle mais celle du parallélogramme ?

par **Carpate** » 19 Déc 2012, 20:40

chacchou a écrit:MB+MC=MA (vecteurs)
mais cela n'est pas la relation de chasle mais celle du parallélogramme ?

On t'a donné la démonstration.
Reprends-la avec papier et crayon : Annick t'en a donné le détail complet
Que veux-tu de plus ?

Un exercice non compris!

un exercice non compris!

Qui est en ligne