Equation du second degré sans delta.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
xxJefffxx
- Membre Naturel
- Messages: 15
- Enregistré le: 19 Nov 2012, 21:10
-
 par xxJefffxx » 25 Nov 2012, 16:15
par xxJefffxx » 25 Nov 2012, 16:15
Bonjour à tous,
Mon problème du jour est que je me suis proposé de résoudre une équation du second degré relativement simple sans utiliser delta et que je ne sais pas vraiment comment m'y prendre !
Si vous pouviez éclairer mon ignorance, je vous en serais grandement reconnaissant.
Voici l'équation : (x-3)²-25/16=0.
Question subsidiaire : quel serait le facteur commun permettant la factorisation de cette fonction :
E(x)=(x²-16)(x+1)+(x+4)(x²-1).
Merci d'avance !
Je vous prie d'agréer mes salutations des plus distinguées,
Jeff'.
-
Khideux
- Membre Naturel
- Messages: 86
- Enregistré le: 30 Nov 2011, 07:50
-
 par Khideux » 25 Nov 2012, 16:24
par Khideux » 25 Nov 2012, 16:24
bonjour,
tu peux remarquer que :
^2-\frac{25}{16})
est du type

et pour la deuxième même chose pour
)
et
)
-
xxJefffxx
- Membre Naturel
- Messages: 15
- Enregistré le: 19 Nov 2012, 21:10
-
 par xxJefffxx » 25 Nov 2012, 16:39
par xxJefffxx » 25 Nov 2012, 16:39
Mes sincères remerciements, cher ami !
-
xxJefffxx
- Membre Naturel
- Messages: 15
- Enregistré le: 19 Nov 2012, 21:10
-
 par xxJefffxx » 25 Nov 2012, 16:41
par xxJefffxx » 25 Nov 2012, 16:41
Par contre, pour la fonction, à quoi cela m'avance-t-il ?
-
Khideux
- Membre Naturel
- Messages: 86
- Enregistré le: 30 Nov 2011, 07:50
-
 par Khideux » 25 Nov 2012, 16:52
par Khideux » 25 Nov 2012, 16:52
xxJefffxx a écrit:Par contre, pour l'équation, à quoi cela m'avance-t-il pour trouver les solutions ?
tu utilises
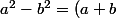(a-b))
donc si tu veux résoudre
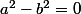
tu auras
(a+b)=0 \Leftrightarrow (a-b)=0 \,\text{ou}\,(a+b)=0)
-
Khideux
- Membre Naturel
- Messages: 86
- Enregistré le: 30 Nov 2011, 07:50
-
 par Khideux » 25 Nov 2012, 16:54
par Khideux » 25 Nov 2012, 16:54
pour la fonction il s'agit pas de résoudre une équation mais de trouver une expression factorisée
-
xxJefffxx
- Membre Naturel
- Messages: 15
- Enregistré le: 19 Nov 2012, 21:10
-
 par xxJefffxx » 25 Nov 2012, 17:02
par xxJefffxx » 25 Nov 2012, 17:02
Merci !
Oui effectivement ! Je m'étais trompé en écrivant rapidement, vous m'en excuserez.
Encore une fois, veuillez agréer mes remerciements distingués !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
