considérons pour
1. Monter que l'on peut écrire
2. En déduire une expression simple de la somme partielle
3. Établir la convergence de la série
1.
2.
3.
je voudrais savoir si la Q 2 et la Q 3 sont correctes merci d'avance .
Exercice série
3 messages
- Page 1 sur 1
exercice série
par gamelle » 31 Oct 2012, 13:30
bonjour j'ai un exercice à faire pour ces vacances et je ne suis pas sûr de ce que j'ai produit
considérons pour
;
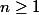
}{(n+1)^2}))
1. Monter que l'on peut écrire
avec )
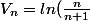2. En déduire une expression simple de la somme partielle
3. Établir la convergence de la série
et calculer la somme.
1.-ln(\frac{n+1}{n+2})=ln(\frac{\frac{n}{n+1}}{\frac{n+1}{n+2}})=ln(\frac{n}{n+1}*\frac{n+2}{n+1})= ln(\frac{n(n+2)}{(n+1)^2}))
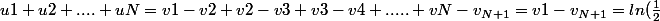2.-ln(\frac{N+1}{N+2})=ln(\frac{\frac{1}{2}}{\frac{N+1}{N+2}})=ln(\frac{1}{2}*\frac{N+2}{N+1})=ln(\frac{N+2}{2(N+1)}))
3.}{(n+1)^2})= ln(\frac{n+2}{2(n+1)})\underset{n \to \infty}{\rightarrow}ln(\frac{1}{2}))
donc la série converge
je voudrais savoir si la Q 2 et la Q 3 sont correctes merci d'avance .
considérons pour
1. Monter que l'on peut écrire
2. En déduire une expression simple de la somme partielle
3. Établir la convergence de la série
1.
2.
3.
je voudrais savoir si la Q 2 et la Q 3 sont correctes merci d'avance .
par arnaud32 » 31 Oct 2012, 13:50
je en vois pas d'erreur si ce l'est qu'il faut ecrire que la somme de ta serie est la limite de ln((n+2)/(2(n+1))
par gamelle » 31 Oct 2012, 14:23
arnaud32 a écrit:je en vois pas d'erreur si ce l'est qu'il faut ecrire que la somme de ta serie est la limite de ln((n+2)/(2(n+1))
okok merci en fait je n'étais pas tres sur pour la question 3
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :