Bonjour,
Je suis soudainement troublé par une situation particulière...
Voici la situation :
La règle de conversion des degré Kelvin vers les degré Celsius est la suivante :
°C = °K - 273.15
Considérons le cas A :
un système est à 300°K il perd 20°K quelle est sa nouvelle température en °C.
Soit :
300°K - 20°K = 280°K
Donc (280-273.15)°C = 6.85°C
Considérons le cas B :
un système est à 300°K il passe brusquement à 280°K quelle fût sa variation de température en °C.
Soit :
280°K - 300°K = (280-273.15)°C - (300-273.15)°C
Donc 280°C - 273.15°C - 300°C + 273.15°C = 280°C - 300°C = -20°C
Ma question est donc la suivante pourquoi dans le cas A la conversion d'unité doit être effectuée après la soustraction et dans le cas B avant ?
Car en effet sinon nous obtiendrions les résultats erronés suivants :
Cas A :
300°K - 20°K = (300 - 273.15)°C - (20 -273.15)°C = 300°C - 273.15°C - 20°C + 273.15°C
soit 300°C - 20°C = 280°C ! ! !
Cas B :
280°K - 300°K = -20°K
soit (-20 - 273.15)°C = -293.15°C ! ! !
Existe-t-il une règle formalisée permettant de déduire dans quel cas la conversion d'unité doit être réalisée avnt la soustraction et dans quel cas après ?
Existe-t-il un concepte mathématique permettant de spécifier que la valeur du cas B est un "delta" et donc n'est pas lié à l'origine de son échelle de mesure ?
Existe-t-il une nuance entre la soustraction aboutissant à un "delta" de valeurs et la soustraction aboutissant à une tierce valeur ?
Merci de vos remarques et suggestions.
Convertion d'unité et soustraction.
11 messages
- Page 1 sur 1
Bonjour,
On travaille ici avec la même unité de mesure ... c'est l'origine zéro qui n'est pas la même mais une augmentation d'un °C ou d'un K est la même chose
Pour ton cas A : 300K est une température , on peut la convertir en °C, le -20 est un delta, c'est au choix des °C ou des K : pas de conversion.
Idem pour ton cas B : -20 est un delta et ne se converti pas.
On travaille ici avec la même unité de mesure ... c'est l'origine zéro qui n'est pas la même mais une augmentation d'un °C ou d'un K est la même chose
Pour ton cas A : 300K est une température , on peut la convertir en °C, le -20 est un delta, c'est au choix des °C ou des K : pas de conversion.
Idem pour ton cas B : -20 est un delta et ne se converti pas.
Bonjour,
Je suis soudainement troublé par une situation particulière...
Voici la situation :
La règle de conversion des degré Kelvin vers les degré Celsius est la suivante :
°C = °K - 273.15
Considérons le cas A :
un système est à 300°K il perd 20°K quelle est sa nouvelle température en °C.
300-273.15-20=6,85 °C
Soit :
300°K - 20°K = 280°K
Donc (280-273.15)°C = 6.85°C
Considérons le cas B :
un système est à 300°K il passe brusquement à 280°K quelle fût sa variation de température en °C.
-20°C
Soit :
280°K - 300°K = (280-273.15)°C - (300-273.15)°C
Donc 280°C - 273.15°C - 300°C + 273.15°C = 280°C - 300°C = -20°C
Ma question est donc la suivante pourquoi dans le cas A la conversion d'unité doit être effectuée après la soustraction et dans le cas B avant ?
Car en effet sinon nous obtiendrions les résultats erronés suivants :
Cas A :
300°K - 20°K = (300 - 273.15)°C - (20 -273.15)°C = 300°C - 273.15°C - 20°C + 273.15°C
soit 300°C - 20°C = 280°C ! ! !
Cas B :
280°K - 300°K = -20°K
soit (-20 - 273.15)°C = -293.15°C ! ! !
Existe-t-il une règle formalisée permettant de déduire dans quel cas la conversion d'unité doit être réalisée avnt la soustraction et dans quel cas après ?
Existe-t-il un concepte mathématique permettant de spécifier que la valeur du cas B est un "delta" et donc n'est pas lié à l'origine de son échelle de mesure ?
Existe-t-il une nuance entre la soustraction aboutissant à un "delta" de valeurs et la soustraction aboutissant à une tierce valeur ?
Merci de vos remarques et suggestions
Je suis soudainement troublé par une situation particulière...
Voici la situation :
La règle de conversion des degré Kelvin vers les degré Celsius est la suivante :
°C = °K - 273.15
Considérons le cas A :
un système est à 300°K il perd 20°K quelle est sa nouvelle température en °C.
300-273.15-20=6,85 °C
Soit :
300°K - 20°K = 280°K
Donc (280-273.15)°C = 6.85°C
Considérons le cas B :
un système est à 300°K il passe brusquement à 280°K quelle fût sa variation de température en °C.
-20°C
Soit :
280°K - 300°K = (280-273.15)°C - (300-273.15)°C
Donc 280°C - 273.15°C - 300°C + 273.15°C = 280°C - 300°C = -20°C
Ma question est donc la suivante pourquoi dans le cas A la conversion d'unité doit être effectuée après la soustraction et dans le cas B avant ?
Car en effet sinon nous obtiendrions les résultats erronés suivants :
Cas A :
300°K - 20°K = (300 - 273.15)°C - (20 -273.15)°C = 300°C - 273.15°C - 20°C + 273.15°C
soit 300°C - 20°C = 280°C ! ! !
Cas B :
280°K - 300°K = -20°K
soit (-20 - 273.15)°C = -293.15°C ! ! !
Existe-t-il une règle formalisée permettant de déduire dans quel cas la conversion d'unité doit être réalisée avnt la soustraction et dans quel cas après ?
Existe-t-il un concepte mathématique permettant de spécifier que la valeur du cas B est un "delta" et donc n'est pas lié à l'origine de son échelle de mesure ?
Existe-t-il une nuance entre la soustraction aboutissant à un "delta" de valeurs et la soustraction aboutissant à une tierce valeur ?
Merci de vos remarques et suggestions
Arnaud-29-31 a écrit:Bonjour,
On travaille ici avec la même unité de mesure ... c'est l'origine zéro qui n'est pas la même mais une augmentation d'un °C ou d'un K est la même chose
Pour ton cas A : 300K est une température , on peut la convertir en °C, le -20 est un delta, c'est au choix des °C ou des K : pas de conversion.
Idem pour ton cas B : -20 est un delta et ne se converti pas.
Bonjour Arnaud,
merci de ta réponse, cependant j'ai énoncé le problème entre °C et °K pour plus de clareté dans les exemples.
Si la situation impliquait °Kelvin et °Fahrenheit alors le delta -20 devrait subir une conversion.
la conversion devrait bien être réalisée avant la soustraction pour le cas B et après pour le cas A.
Ma question porte sur un formalisme permettant de détecter quand est-ce que la soustraction nous fournit une valeur liée à l'origine et quand est-ce qu'elle nous fournit un "delta" non lié à l'origine.
Ou encore quand pert-on cette notion de "relatif à l'origine" ?
Je ne suis pas sur qu'une telle distinction existe...
annick a écrit:Bonjour,
pour appuyer ce que vient de dire Arnaud, tu remarqueras que la différence entre tes deux résultats est...273,15.
Annick et Arnaud je suis d'accord avec vous et je sais bien que le résultat est faux suivant que l'on effectue les conversions avant ou après la soustraction.
Ma question porte sur un éventuel formalisme permettant de distinguer ces deux cas.
Comment expliquer à quelqu'un la raison pour laquelle dans un cas la conversion doit être effectuée avant et dans un autre la conversion doit être effectuée après ?
au départ nous effectuons une simple soustraction entre deux valeurs de même unités.
Dans un cas nous effectuons Valeur - Delta => Valeur
et dans l'autre Valeur - Valeur => Delta.
Cette notion de "Delta" et donc de perte de la relativité à l'origine existe-telle en mathématique ?
Arnaud-29-31 a écrit:Encore une fois, faire la conversion avant ou après l'opération de change rien pourvu que l'on ne fasse pas de fausse conversion.
Fais l'analogie avec les points et les distances
Arnaud, encore une fois merci de ta réponse mais ce qui me turlupine en ce moment n'est pas de trouver quand effectuer la conversion, effectivement quand nous sommes face à un "delta" et quand nous sommes face à une valeur nous savons comment convertir.
Ce qui me rends insatisfait c'est ceci :
Soit N = 200°K - 30°K
il est impossible de calculer N en °C !
pour pouvoir effectuer la convertion °K vers °C il faudrait connaître la nature de la valeur résultant de la soustraction :
un "delta" => pas de convertion par rapport à l'origine mais convertion de la graduation (ex : °F vers °C)
une valeur => convertion totale : origine et au besoin graduation.
Je suis donc surpris qu'apparement les mathématiques n'ait pas créé un indicateur formel permettant d'identifier cette nature...
En tout cas je n'en connais pas...
Eh bien si ... la différence réside dans la manière de le dire, ce ne sont pas les même objets.
Prends des points et des distances c'est la même chose.
D'autre part on fait du numérique (interdit en math avant la dernière ligne où l'on écrit AN : ....) c'est peut-être la qu'apparait la confusion, tant que l'on garde des notations mathématiques on aura des température ( ) et des variations de température (
) et des variations de température (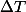 ) et pas de confusion possible entre un écart entre deux température et une température modifiée d'un écart.
) et pas de confusion possible entre un écart entre deux température et une température modifiée d'un écart.
Prends des points et des distances c'est la même chose.
D'autre part on fait du numérique (interdit en math avant la dernière ligne où l'on écrit AN : ....) c'est peut-être la qu'apparait la confusion, tant que l'on garde des notations mathématiques on aura des température (
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
