Limites, valeur absolue ...

[Samiiia]

Bonjour,

Je suis en ce moment sur l'exercice suivant :

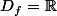
Soit f la fonction définie sur / {-1} par

1° En considérant différents intervalles, donner l'écriture de sans valeur absolue.

2° En déduire et

Mes problèmes :

1° Est-ce qu'il faut utiliser la partie entière pour se débarrasser de la valeur absolue ? J'ai entendu dire que c'était la même chose. Mais même en essayant, je n'y arrive pas. De plus, je ne sais pas quels intervalles traiter, même en visualisant sur la calculatrice. J'ai l'intervalle )-1;1) mais après cela se réduit à une infinité de points sur une parabole. Je ne sais pas comment les traiter.

2° Je pense pouvoir trouver la limite.

Merci d'avance.

[Manny06]

Bonjour,

Je suis en ce moment sur l'exercice suivant :

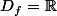
Soit f la fonction définie sur / {1} par

1° En considérant différents intervalles, donner l'écriture de sans valeur absolue.

2° En déduire et

Mes problèmes :

1° Est-ce qu'il faut utiliser la partie entière pour se débarrasser de la valeur absolue ? J'ai entendu dire que c'était la même chose. Mais même en essayant, je n'y arrive pas. De plus, je ne sais pas quels intervalles traiter, même en visualisant sur la calculatrice. J'ai l'intervalle )-1;1) mais après cela se réduit à une infinité de points sur une parabole. Je ne sais pas comment les traiter.

2° Je pense pouvoir trouver la limite.

Merci d'avance.

Pour se "débarasser de la valeur absolue il faut étudier le signe de (x²-1) que tu peux factoriser en (x-1)(x+1)

fais donc un tableau de signe

[Black Jack]

x²-1 = (x-1)(x+1)

x²-1 >= 0 si x est dans ]-oo ; -1] ou dans [1 ; +oo[
x²-1 < 0 si x est dans ]-1 ; 1[

|x²-1| = x²-1 si x est dans ]-oo ; -1] ou dans [1 ; +oo[
|x²-1| = 1-x² si x est dans ]-1 ; 1[

Il faut donc considérer les 3 intervalles :

a) ]-oo ; -1[ (le -1 exclu à cause du (x+1) au dénominateur de f(x))
b) ]-1 ; 1[
c) [1 ; +oo[

Dans le ou les intervalles où (x²-1) >= 0, il faut remplacer |x²-1| par (x²-1) dans l'expression de f(x)
Et dans le ou les intervalles où (x²-1) < 0, il faut remplacer |x²-1| par (1-x²) dans l'expression de f(x)

Essaie ...

:zen:

[Samiiia]

x²-1 = (x-1)(x+1)

x²-1 >= 0 si x est dans ]-oo ; -1] ou dans [1 ; +oo[
x²-1 = 0, il faut remplacer |x²-1| par (x²-1) dans l'expression de f(x)
Et dans le ou les intervalles où (x²-1) < 0, il faut remplacer |x²-1| par (1-x²) dans l'expression de f(x)

Essaie ...

:zen:

Merci à vous deux, pour vos réponses.

J'ai obtenu ceci :

Sur ]-oo ; -1[, on a

Sur ]-1 ; 1[, on a

Sur [1 ; +oo[, on a

Est-ce juste ?

2° Pour les limites, est-ce que quand on est dans ]-oo ; -1[, le numérateur : tend vers +oo et le dénominateur : tend vers -oo. Si oui, alors je dois factoriser par le terme de plus haut degré pour trouver la limite ?

[Samiiia]

Merci à vous deux, pour vos réponses.

J'ai obtenu ceci :

Sur ]-oo ; -1[, on a

Sur ]-1 ; 1[, on a

Sur [1 ; +oo[, on a

Est-ce juste ?

2° Pour les limites, est-ce que quand on est dans ]-oo ; -1[, le numérateur : tend vers +oo et le dénominateur : tend vers -oo. Si oui, alors je dois factoriser par le terme de plus haut degré pour trouver la limite ?

Est-ce que quelqu'un pourrait me répondre, s'il vous plait ?

[Manny06]

Est-ce que quelqu'un pourrait me répondre, s'il vous plait ?

x²-1=(x-1)(x+1)
tu peux simplifier la fraction