Limite de suite

[LOLO64]

On considère la suite vn définie sur N par vn=3-un et un+1 = racine de 3un
1) vérifiez que pour tout entier naturel n, vn+1= racine3* (3-Un/racineUn + racine de 3 )

2) Démontrer que pour tout entier naturel n , vn+1 < ou égale à[ racine de 3 / (1+racine de 3 ) ]vn

3) Démontrer par récurrence , que pour tout entier naturel n , vn< ou égale à 2(racine de 3/1+racine de 3) ^n

4) déduisez en la limite de la suite (vn) puis celle de la suite (un)

[raito123]

Oui ?? C'est quoi le problème ?

[tototo]

On considère la suite vn définie sur N par vn=3-un et un+1 = racine de 3un
1) vérifiez que pour tout entier naturel n, vn+1= racine3* (3-Un/racineUn + racine de 3 )
vn+1=3-un+1 =3-racine de 3un=racine3* (3-Un/racineUn + racine de 3 )
2) Démontrer que pour tout entier naturel n , vn+1 < ou égale à[ racine de 3 / (1+racine de 3 ) ]vn

3) Démontrer par récurrence , que pour tout entier naturel n , vn< ou égale à 2(racine de 3/1+racine de 3) ^n

4) déduisez en la limite de la suite (vn) puis celle de la suite (un)

[Anonyme]

@LOLO64
Voici quelques commentaires sur ton énoncé

1) une suite dite récurrente par exemple n'est définie que si on donne son 1er terme par exemple
2) Pourquoi ne pas étudier la suite et calculer sa limite (si elle existe )
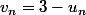3) Une fois qu'on "connait" la suite alors la relation permet de "connaitre" la suite

Cela ne répond pas aux questions de ton exercice (qui sont à mon avis inutilement compliquées)

La méthode que je te propose de suivre est plus simple ( et plus classique ) que ton énoncé

Dans les 2 méthodes an arrive au même résultat :
la suite converge vers 3 et la suite converge vers 0

A toi de voir ce qu'il faut travailler et surtout comment ?

[Anonyme]

@tototo
J'ai remarqué à dans "multes discussions" , tu participes à des discussions UNIQUEMENT en recopiant le sujet de l'auteur !

et BIEN SUR cela m'intrigue....

Quel est le message que tu veux faire passer en faisant cela ?
Merci pour tes explications

[raito123]

Il est ...comment on dirait ... très actif !!

[LOLO64]

Bonjour,


Merci de votre aide !

Pour la première question que j'ai travaillé , j'ai commencé par noté Vn+1=3-Un+1 et je l'ai ainsi remplacé dans l'expression !