Fonction caractéristique d'un ensemble
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 13:36
par guigui130 » 15 Sep 2012, 13:36
Bonjours
voila lénonce de mon problème :
On se place dans un ensemble E "universel"
La fonction caractéristique d'un sous ensemble A c E est la fonction Q:E-->{0,1} qui prend la valeur 1 sur les élément de A et la valeur 0 sur les élément E\A
Montrer que QAnB=QAQB, que QAuB=QA +QB-QAQB, et que QA\B=QA-QAQB
Déjà je ne sais pas si il faut raisonner avec les valeur 1 ou 0 ou montrer l'inclusion des ensembles merci de m'indiquer la démarche a suivre
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 13:39
par Luc » 15 Sep 2012, 13:39
Salut,
pour montrer l'égalité de deux fonctions, il suffit de la vérifier sur tous les points de leur ensemble de définition.
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 13:41
par guigui130 » 15 Sep 2012, 13:41
Donc il faut raisonner avec les valeur 1 ou 0 ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 13:45
par Luc » 15 Sep 2012, 13:45
guigui130 a écrit:Donc il faut raisonner avec les valeur 1 ou 0 ?
Quel est l'ensemble de définition des fonctions dont tu veux montrer l'égalité?
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 13:48
par guigui130 » 15 Sep 2012, 13:48
on se trouve dans un ensemble dit "universelle" donc il contient tous type d'ensemble
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 13:58
par guigui130 » 15 Sep 2012, 13:58
je traduit la fonction pour ceux qui n'ont pas compris Q--->{0,1}
x --> 1 pour x appartenant a A
x --> 0 pour x nappartenant pas a A
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 14:00
par Luc » 15 Sep 2012, 14:00
guigui130 a écrit:on se trouve dans un ensemble dit "universelle" donc il contient tous type d'ensemble
L'ensemble E contient des éléments. Pour calculer l'image d'un élément de E par une fonction caractéristique d'un sous-ensemble A, il suffit de savoir si
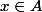
ou non.
Donc tu peux regarder si QAnB(x)=QA(x)QB(x) pour

, et ensuite dans le complémentaire pour voir si cette égalité de fonctions est vraie.
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 14:09
par guigui130 » 15 Sep 2012, 14:09
oui je suis d'accord AnB signifie que x appartiens a l'ensemble A donc QAnB=1 mais que signifie QAQB est ce que QAQB=QA*QB ? si c'est cela QA*QB=1*0=0 donc légalité AnB=QAQB est fausse ou alors QAQB={1,0} mais dans se cas la légalité s'avère fausse
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 14:10
par Luc » 15 Sep 2012, 14:10
guigui130 a écrit:oui je suis d'accord AnB signifie que x appartiens a l'ensemble A donc QAnB=1 mais que signifie QAQB est ce que QAQB=QA*QB ? si c'est cela QA*QB=1*0=0 donc légalité AnB=QAQB est fausse ou alors QAQB={1,0} mais dans se cas la légalité s'avère fausse
Sois plus précis parce que là ce que tu dis n'a aucune sens mathématique malheureusement. Tu écris des égalités d'ensembles et de fonctions, de nombres et de fonctions...
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 14:11
par guigui130 » 15 Sep 2012, 14:11
Luc a écrit:Sois plus précis parce que là ce que tu dis n'a aucune sens mathématique malheureusement. Tu écris des égalités d'ensembles et de fonctions, de nombres et de fonctions...
Es tu d'accord pour dire que QAnB=1 ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 14:13
par Luc » 15 Sep 2012, 14:13
guigui130 a écrit:Es tu d'accord pour dire que QAnB=1 ?
Une fonction égale à un nombre?
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 14:16
par guigui130 » 15 Sep 2012, 14:16
Luc a écrit:Une fonction égale à un nombre?
Be moi j'ai compris que Q attribu une valeur au ensemble soit 1 ou 0
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 14:37
par Luc » 15 Sep 2012, 14:37
guigui130 a écrit:Be moi j'ai compris que Q attribu une valeur au ensemble soit 1 ou 0
Q n'est pas une fonction définie sur E, mais sur P(E). Q prend une partie de E et lui associe sa fonction caractéristique Q_A. Q_A est une fonction définie sur E, c'est la fonction caractéristique de A
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 14:50
par guigui130 » 15 Sep 2012, 14:50
Luc a écrit:Q n'est pas une fonction définie sur E, mais sur P(E). Q prend une partie de E et lui associe sa fonction caractéristique Q_A. Q_A est une fonction définie sur E, c'est la fonction caractéristique de A
donc pour montrer légalité suivante QAnB=QAQB il faut raisonner en terme d'inclusion ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 14:51
par Luc » 15 Sep 2012, 14:51
guigui130 a écrit:donc pour montrer légalité suivante QAnB=QAQB il faut raisonner en terme d'inclusion ?
Non, il faut montrer que les fonctions QAnB et QAQB sont égales.
-
guigui130
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2012, 13:19
-
 par guigui130 » 15 Sep 2012, 14:54
par guigui130 » 15 Sep 2012, 14:54
Luc a écrit:Non, il faut montrer que les fonctions QAnB et QAQB sont égales.
Qu'elle est la démarche a suivre parce que je vois pas du tous comment mi prendre
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 14:58
par Luc » 15 Sep 2012, 14:58
guigui130 a écrit:Qu'elle est la démarche a suivre parce que je vois pas du tous comment mi prendre
Tu prends un élément x de E, et tu montres que QAnB(x)=QA(x)QB(x).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
