Je ne sais pas comment m'y prendre pour trouver cette limite, j'attend votre aide
La fonction est :
f(x) = (2-x)^tan((pi/2)x)
et la limite est à trouver lorsque x tend vers 1 par valeurs inférieures.
Limite en 1- avec tan
5 messages
- Page 1 sur 1
par M@thIsTheBest » 11 Juin 2012, 16:35
Anko a écrit:Je ne sais pas comment m'y prendre pour trouver cette limite, j'attend votre aide
La fonction est :
f(x) = (2-x)^tan((pi/2)x)
et la limite est à trouver lorsque x tend vers 1 par valeurs inférieures.
Tu veux dire
par M@thIsTheBest » 11 Juin 2012, 16:42
Anko a écrit:Je ne sais pas comment m'y prendre pour trouver cette limite, j'attend votre aide
La fonction est :
f(x) = (2-x)^tan((pi/2)x)
et la limite est à trouver lorsque x tend vers 1 par valeurs inférieures.
C'est
par cuati » 11 Juin 2012, 19:37
Bonsoir,
=exp ( \tan( \frac{\pi x}{2}) \ln(2-x) ))
on cherche la limite en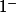 
ce qui revient à chercher la limite en 
avec le changement de variable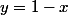 
. Soit la limite quand 
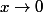de }{2}) \ln(1+x) ))
.
Il suffit donc ici de trouver la limite en 0 de}{2}) \ln(1+x))
.... (elle est finie).
On utilise le fait que}{2})=\frac{1}{\tan(\frac{\pi x}{2})})
et après il n'y a plus qu'à prendre des équivalents en 0 pour conclure que la limite de 
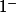en est 
Il suffit donc ici de trouver la limite en 0 de
On utilise le fait que
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :