Equations trigonométriques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 16:35
par Maxime-59 » 30 Avr 2012, 16:35
Bonjour,
Je viens ici car j'ai un exercice dans lequel je dois résoudre 5 équations trigonométriques mais je suis incapable de les résoudres ... Pourriez-vous m'aider en me mettant sur la voie ?
1)
 = cos (x+\frac{\Pi}{3}))
2)
 -1 = 0)
3)
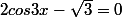
4)
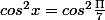
5)
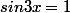
J'ai regardé dans mon cours, dans mon livre, aucune info ou alors les exemples du livres ne m'aident pas pour résoudre ces équations ...
Merci de votre aide
-
lol37
- Membre Relatif
- Messages: 139
- Enregistré le: 17 Avr 2010, 13:39
-
 par lol37 » 30 Avr 2012, 16:44
par lol37 » 30 Avr 2012, 16:44
Maxime-59 a écrit:Bonjour,
Je viens ici car j'ai un exercice dans lequel je dois résoudre 5 équations trigonométriques mais je suis incapable de les résoudres ... Pourriez-vous m'aider en me mettant sur la voie ?
1)
 = cos (x+\frac{\Pi}{3}))
2)
 -1 = 0)
3)
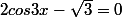
4)
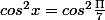
5)
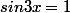
J'ai regardé dans mon cours, dans mon livre, aucune info ou alors les exemples du livres ne m'aident pas pour résoudre ces équations ...
Merci de votre aide
Salut,
Tu peux appliquer les fonctions réciproques pour te ramener à une équation affine que tu sais résoudre.
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Avr 2012, 16:44
par annick » 30 Avr 2012, 16:44
Bonjour,
pour la 1), je suppose que tu as quand même dans ton cours cosa=cob donc a=....
pour la 2), pense que 1/2 est un sinus connu
pour la 3) pense que V3/2 est un cosinus connu.
pour la 5), pense que 1 est un sinus connu
pour la 4)a²-b²=
Voici quelques pistes
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Avr 2012, 16:47
par Carpate » 30 Avr 2012, 16:47
Maxime-59 a écrit:Bonjour,
Je viens ici car j'ai un exercice dans lequel je dois résoudre 5 équations trigonométriques mais je suis incapable de les résoudres ... Pourriez-vous m'aider en me mettant sur la voie ?
1)
 = cos (x+\frac{\Pi}{3}))
2)
 -1 = 0)
3)
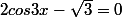
4)
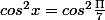
5)
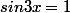
J'ai regardé dans mon cours, dans mon livre, aucune info ou alors les exemples du livres ne m'aident pas pour résoudre ces équations ...
Merci de votre aide
Bonsoir,
Ces exercices demandent une étude préalable du cours !
1) Quelle relation lie 2 angles qui ont le même cosinus (trace les sur le cercle trigonométrique) ?
2) sin(x - pi/4) = 1
Quel est l'angle dont le sinus vaut 1 ?
3) cos(3) = rac(3) /2
Quel est l'angle dont le cosinus vaut rac(3) /2 ?
4) de la forme a^2 - b^2 : factoriser
5) sin(3x) = 1
Quel est l'angle dont le sinus vaut 1 ?
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 17:06
par Maxime-59 » 30 Avr 2012, 17:06
Woaw ! ça fait plaisir de voir autant de réponses en un si petit laps de temps, cool de voir qu'il y a des gens disponibles et prêt à aider !
Je sais que :
 = 1)
Donc pour la 5eme, ça pourrait me faire :
 = Sin(\frac{\pi}{2}))
?
J'ai regardé un cours tout à l'heure qui disait qu'il fallait s'arranger pour transformer l'écriture de droite en sinus, voilà chose faite donc mais quoi faire maintenant ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Avr 2012, 17:14
par Carpate » 30 Avr 2012, 17:14
Maxime-59 a écrit:Woaw ! ça fait plaisir de voir autant de réponses en un si petit laps de temps, cool de voir qu'il y a des gens disponibles et prêt à aider !
Je sais que :
 = 1)
Donc pour la 5eme, ça pourrait me faire :
 = Sin(\frac{\pi}{2}))
?
J'ai regardé un cours tout à l'heure qui disait qu'il fallait s'arranger pour transformer l'écriture de droite en sinus, voilà chose faite donc mais quoi faire maintenant ?
Et si tu lis plus attentivement ton cours tu verras que sin a = sin b se résout en
a= b
a = pi - b
Il n'est pas interdit de griffonner un petit dessin avec sur le cercle trigonométrique 2 points A et B extrémités d'arcs ayant même sinus : A et B confondus ou symétriques par rapport à l'axe des ordonnées ...
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 30 Avr 2012, 17:14
par Kikoo <3 Bieber » 30 Avr 2012, 17:14
Maxime-59 a écrit:Woaw ! ça fait plaisir de voir autant de réponses en un si petit laps de temps, cool de voir qu'il y a des gens disponibles et prêt à aider !
Je sais que :
 = 1)
Donc pour la 5eme, ça pourrait me faire :
 = Sin(\frac{\pi}{2}))
?
J'ai regardé un cours tout à l'heure qui disait qu'il fallait s'arranger pour transformer l'écriture de droite en sinus, voilà chose faite donc mais quoi faire maintenant ?
Yo,
Ben tu appliques ce qu'il y a dans ton cours.
sin(a)=sin(b) a=... ou a=...
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Avr 2012, 17:16
par annick » 30 Avr 2012, 17:16
Tout d'abord, je doute que tu aies ce type d'équations à résoudre sans avoir le cours qui te dis que si :
cosa=cosb, alors a=b+2kpi ou.....
De même pour sina=sinb.
Mais, si c'est le cas, tu peux toujours essayer de réfléchir en utilisant le cercle trigonométrique : sur ton cercle, quelles sont les deux façons d'avoir sin a= sinb et quelles sont les deux façons d'avoir cosa=cosb ?
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 17:47
par Maxime-59 » 30 Avr 2012, 17:47
Alors, je récapitule :
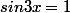
 = Sin(\frac{\pi}{2}))
Et là je comprends rien avec les "
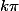
" ...
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 30 Avr 2012, 17:52
par Kikoo <3 Bieber » 30 Avr 2012, 17:52
Maxime-59 a écrit:Alors, je récapitule :
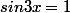
 = Sin(\frac{\pi}{2}))

?
Nan. Si tu traces le cercle trigo, tu vois bien qu'un sinus donné admet deux solutions modulo 2pi.
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 17:58
par Maxime-59 » 30 Avr 2012, 17:58
Sur le cour fourni dans mon livre j'ai un exemple qui est :
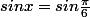
Les solutions cette équation trigonométrique sont :

Je n'arrive pas à me servir de cet exemple pour résoudre mon équation
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 19:06
par Maxime-59 » 30 Avr 2012, 19:06
Je cherche, je cherche mais je ne trouve toujours pas ...
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 19:28
par Maxime-59 » 30 Avr 2012, 19:28
D'après ce que je vois sur le cour, les solution sont :
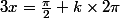
et
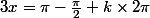
C'est bon ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Avr 2012, 19:49
par Carpate » 30 Avr 2012, 19:49
Maxime-59 a écrit:D'après ce que je vois sur le cour, les solution sont :
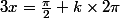
et
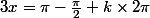
C'est bon ?
Ouf ! Ca y est presque ...
3x = pi/2 et 3x = pi - pi/2 fournissent la même solution :
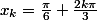
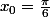
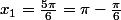
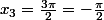
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 20:00
par Maxime-59 » 30 Avr 2012, 20:00
Je comprends pas ce que tu viens de dire

-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 30 Avr 2012, 20:10
par Kikoo <3 Bieber » 30 Avr 2012, 20:10
Maxime-59 a écrit:Je comprends pas ce que tu viens de dire

Il vient de t'initier à la notion du modulo !

Sur le cercle trigo,

et
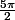
sont les "mêmes" angles modulo

-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 20:13
par Maxime-59 » 30 Avr 2012, 20:13
Donc ma réponse n'est pas bonne ? :/
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 30 Avr 2012, 20:23
par Kikoo <3 Bieber » 30 Avr 2012, 20:23
Maxime-59 a écrit:Donc ma réponse n'est pas bonne ? :/
Tu étais sur la bonne voie ! Il ne te reste plus qu'à isoler x, ce qui, tu me l'avoueras, n'est pas bien compliqué ^^
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 20:37
par Maxime-59 » 30 Avr 2012, 20:37
Il suffit donc de tout multiplier par 1/3, en effet, ça parait pas bien compliqué !
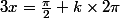
et
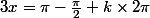
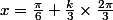
et
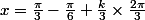
Je ne suis pas sur dans le mesure ou je ne sais pas si le "k" doit aussi être multiplié, je pense que oui mais bon ..
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 30 Avr 2012, 21:13
par Kikoo <3 Bieber » 30 Avr 2012, 21:13
Maxime-59 a écrit:Il suffit donc de tout multiplier par 1/3, en effet, ça parait pas bien compliqué !
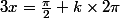
et
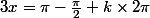
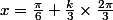
et
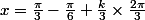
Je ne suis pas sur dans le mesure ou je ne sais pas si le "k" doit aussi être multiplié, je pense que oui mais bon ..
En effet, tu as raison de douter

On a
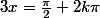
et
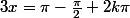
D'où
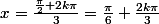
et la même chose pour l'autre relation.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
