Integrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 21 Mar 2012, 19:08
par mec59 » 21 Mar 2012, 19:08
bonjour a tous j'ai un exercice avec 4 integrales mais 2 me posent probleme :

et
^3} dx)
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 21 Mar 2012, 19:18
par Euler07 » 21 Mar 2012, 19:18
mec59 a écrit:bonjour a tous j'ai un exercice avec 4 integrales mais 2 me posent probleme :

et
^3} dx)
Pour la première : cos²x + sin²x = 1 et pense à tan x = sin x / cos x
:livre:
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 21 Mar 2012, 19:33
par ev85 » 21 Mar 2012, 19:33
mec59 a écrit:bonjour a tous j'ai un exercice avec 4 integrales mais 2 me posent probleme :

et
^3} dx)
Pour la deuxième

emballez, c'est pesé.
e.v.
-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 21 Mar 2012, 19:45
par mec59 » 21 Mar 2012, 19:45
donc la premiere deviendrai

=

-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 21 Mar 2012, 19:47
par mec59 » 21 Mar 2012, 19:47
ev85 a écrit:Pour la deuxième

emballez, c'est pesé.
e.v.
je ne comprend pas ,
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 21 Mar 2012, 20:04
par Euler07 » 21 Mar 2012, 20:04
mec59 a écrit:donc la premiere deviendrai

=

Oui :we:
:livre:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 21 Mar 2012, 20:08
par Skullkid » 21 Mar 2012, 20:08
mec59 a écrit:je ne comprend pas ,
Bonjour, ev85 te propose de faire le changement de variable u = t². Une autre méthode est de repérer que l'intégrande est presque de la forme
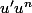
.
-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 21 Mar 2012, 20:16
par mec59 » 21 Mar 2012, 20:16
Euler07 a écrit:Oui :we:
:livre:
d'accord jai terminer celle la

il me reste la 2nd

-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 21 Mar 2012, 20:19
par mec59 » 21 Mar 2012, 20:19
Skullkid a écrit:Bonjour, ev85 te propose de faire le changement de variable u = t². Une autre méthode est de repérer que l'intégrande est presque de la forme
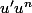
.
justement j'ai du mal a voir une forme u' u^n

-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 21 Mar 2012, 20:22
par Skullkid » 21 Mar 2012, 20:22
À ton avis qu'est-ce que ça pourrait être ce u, en regardant la tête de l'intégrande ?
-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 21 Mar 2012, 20:36
par mec59 » 21 Mar 2012, 20:36
Skullkid a écrit:À ton avis qu'est-ce que ça pourrait être ce u, en regardant la tête de l'intégrande ?
'ai trouver c'est bon et jai verifier grace a la calculatrice merci bq , mais par contre vu que les bone de l'interale son 0 et x je m'arrete juste apré la recherche de primitive ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 21 Mar 2012, 21:03
par Skullkid » 21 Mar 2012, 21:03
Que les bornes s'appellent a et b ou 0 et x ça change pas grand chose :
dt = f(x)-f(0))
.
-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 21 Mar 2012, 22:23
par mec59 » 21 Mar 2012, 22:23
Skullkid a écrit:Que les bornes s'appellent a et b ou 0 et x ça change pas grand chose :
dt = f(x)-f(0))
.
mais on ne peu pa aller plus loin parceque x n'est pazs une valeur si ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 21 Mar 2012, 22:28
par Skullkid » 21 Mar 2012, 22:28
x c'est un nombre comme un autre, c'est juste que tu n'as pas sa valeur numérique, mais ça ne t'empêche pas de faire des calculs dessus et d'exprimer f(x).
-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 22 Mar 2012, 16:15
par mec59 » 22 Mar 2012, 16:15
Skullkid a écrit:x c'est un nombre comme un autre, c'est juste que tu n'as pas sa valeur numérique, mais ça ne t'empêche pas de faire des calculs dessus et d'exprimer f(x).
mais je n'arrive pas a simplifier
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 22 Mar 2012, 17:21
par Skullkid » 22 Mar 2012, 17:21
Montre moi ce que tu as fait.
-
mec59
- Membre Naturel
- Messages: 59
- Enregistré le: 08 Sep 2010, 19:27
-
 par mec59 » 22 Mar 2012, 20:39
par mec59 » 22 Mar 2012, 20:39
Skullkid a écrit:Montre moi ce que tu as fait.
je trouve
^2} \big]_0 ^x)
^2}-\frac{-1}{2(0^2+1)^2} \big]_0 ^x)
^2}+\frac{1}{2} \big]_0 ^x)
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 22 Mar 2012, 23:58
par Skullkid » 22 Mar 2012, 23:58
Pourquoi tu gardes les

à partir de la deuxième ligne ? Une fois que tu t'es débarrassé de ta variable muette t, ils disparaissent. Bref, ce que tu as écrit est quasiment bon, y a juste les

qui ne devraient pas être là.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
