Décomposition en éléments simples
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 19:43
par mitron » 04 Fév 2012, 19:43
Bonjour,
je cherche à décomposer en éléments simples la fraction rationnelle suivante:

.
En décomposant

, je trouve:
} + \frac{2}{3(x^2 + x +1)})
puis j'ai multiplié par x, mais apparemment ce n'est pas bon car dans la correction, je suis censé trouver:
} + \frac{x-1}{3(x^2 + x +1)})
Quelqu'un peut m'aider? Merci.
PS: la décomposition en éléments simples n'est pas au programme PC/PCSI.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 04 Fév 2012, 19:46
par Le_chat » 04 Fév 2012, 19:46
mitron a écrit:Bonjour,
je cherche à décomposer en éléments simples la fraction rationnelle suivante:

.
En décomposant

, je trouve:
} + \frac{2}{3(x^2 + x +1)})
puis j'ai multiplié par x, mais apparemment ce n'est pas bon car dans la correction, je suis censé trouver:
} + \frac{x-1}{3(x^2 + x +1)})
Quelqu'un peut m'aider? Merci.
PS: la décomposition en éléments simples n'est pas au programme PC/PCSI.
Ben ouais mais quand tu vas multiplier par x, tu auras un x/3(1-x), qui n'est pas un élément simple (il est de degré 0).
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 19:51
par mitron » 04 Fév 2012, 19:51
Oui, mais alors comment fait-on pour parvenir à la relation ci-dessus?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 19:55
par SaintAmand » 04 Fév 2012, 19:55
mitron a écrit:En décomposant

, je trouve:
} + \frac{2}{3(x^2 + x +1)})
Ce n'est pas correct.
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 19:58
par mitron » 04 Fév 2012, 19:58
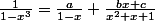
et je trouve a = 1/3, c = 2/3 et b = 0.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 20:08
par SaintAmand » 04 Fév 2012, 20:08
mitron a écrit: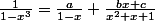
et je trouve a = 1/3, c = 2/3 et b = 0.
 }+\frac{1}{3\left( 1-x\right)}=\frac{x^{2}-x+3}{3(1-x^3)})
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 20:11
par mitron » 04 Fév 2012, 20:11
Ah oui j'ai fais un erreur de calcul. Pour le premier terme, j'ai au numérateur: -x +2 avec b = -1/3.
Mais alors comment dois-je procéder pour avoir l'expression désirée?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 20:17
par SaintAmand » 04 Fév 2012, 20:17
mitron a écrit:Ah oui j'ai fais un erreur de calcul. Pour le premier terme, j'ai au numérateur: -x +2 avec b = -1/3.
Mais alors comment dois-je procéder pour avoir l'expression désirée?
Ok pour a. Pour b et c, regarde la limite en +infini après avoir multiplié les membres par x, et la limite en 0.
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 20:21
par mitron » 04 Fév 2012, 20:21
J'ai beau refaire les calculs je trouve toujours b=-1/3 et c=2/3... mais le x au numérateur me pose problème.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 20:28
par SaintAmand » 04 Fév 2012, 20:28
mitron a écrit:J'ai beau refaire les calculs je trouve toujours b=-1/3 et c=2/3... mais le x au numérateur me pose problème.
D'accord pour c. Pour b vérifie ton calcul, tu brûles.
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 20:33
par mitron » 04 Fév 2012, 20:33
b=1/3
mais pour le x, on fait comment?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 20:46
par SaintAmand » 04 Fév 2012, 20:46
mitron a écrit:b=1/3
mais pour le x, on fait comment?
J'étais sur la décomposition de

. Pour

, tu peux employer les mêmes méthodes. Pour b tu poses x=0 et pour c tu prends la limite en +infini après avoir multiplié par x.
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 20:57
par mitron » 04 Fév 2012, 20:57
Vous pourriez détailler svp?
Quand je veux poser b=0, je n'ai plus le b puisque j'ai du bx²
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 21:09
par SaintAmand » 04 Fév 2012, 21:09
mitron a écrit:Vous pourriez détailler svp?
Quand je veux poser b=0, je n'ai plus le b puisque j'ai du bx²
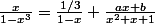
Pose x=0 dans l'égalité précédentes; tu obtiens
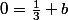
Multiplie les deux membres par x et fais tendre x en +infini; tu obtiens
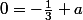
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 21:11
par mitron » 04 Fév 2012, 21:11
On a toujours:

=

?
Si on avait au numérateur 2, ou x, ou x², on aurait toujours cette décomposition?
Merci.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 21:17
par SaintAmand » 04 Fév 2012, 21:17
mitron a écrit:On a toujours:

=

?
Oui.
Si on avait au numérateur 2, ou x, ou x², on aurait toujours cette décomposition?
Soit plus explicite. N'as-tu pas de livres sous la main ?
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 21:20
par mitron » 04 Fév 2012, 21:20
La décomposition en éléments simples n'est pas à mon programme, alors je me suis renseigné sur Internet.
Ce que je veux dire c'est que le terme au numérateur (réel, monôme en x/x² ou polynôme) ne change rien à la décomposition?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 21:29
par SaintAmand » 04 Fév 2012, 21:29
mitron a écrit:La décomposition en éléments simples n'est pas à mon programme, alors je me suis renseigné sur Internet.
À la bibliothèque de ton lycée il doit surement y avoir les manuels d'Arnaudiès & Fraysse. Sinon
http://stephane.gonnord.org/PCSI/Algebre/FRACTIONS.PDF Ce que je veux dire c'est que le terme au numérateur (réel, monôme en x/x² ou polynôme) ne change rien à la décomposition?
Bien sur que si.
-
mitron
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Déc 2011, 15:13
-
 par mitron » 04 Fév 2012, 21:35
par mitron » 04 Fév 2012, 21:35
Si on a un x² au numérateur par exemple, on a toujours:

=

en gros, seuls a,b et c changent. Mais la décomposition reste la même?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Fév 2012, 22:15
par SaintAmand » 04 Fév 2012, 22:15
mitron a écrit:Si on a un x² au numérateur par exemple, on a toujours:

=

en gros, seuls a,b et c changent. Mais la décomposition reste la même?
Si la fraction est irréductible, la forme de la factorisation est déterminée par la factorisation en polynômes irréductibles du dénominateur. Évidemment le corps (R ou C généralement) a son importance.
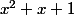
est un polynôme irréductible de R[X] mais pas de C[X].
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
.
, je trouve:
puis j'ai multiplié par x, mais apparemment ce n'est pas bon car dans la correction, je suis censé trouver:
} + \frac{x-1}{3(x^2 + x +1)})
=
