Raisonner et démontrer (trigonométrie de 1ere)

[Loan]

Bonsoir à toutes et à tous, je remercie d'avance ceux qui m’aideront ! Voilà un exercice sur lequel je bloque. En fait je "sais" les réponses mais je ne sais pas comment les démontrer ou expliquer la façon dont je les trouve! Voici l'énoncé :

Le but de l'exercice est de résoudre l'équation (E) : cos 3x = 0
1.a) Démontrer que x est solution de (E) si et seulement si 3x= (;)/2)+k2;) et 3x= -(;)/2)+k2;) avec k en entier relatif.
Je sais que les seuls points se situant sur l'axe des sinus (et donc d'abscisse 0) se trouvent en /2 et -;)/2 et que quelque soit le nombre de tours ajouté on retombe sur le même point. Mais comment l'expliquer dans un "langage mathématique" ?

b) Écrire les solutions de l'équation (E).
Les solutions sont donc -(;)/2)+k2;) et (;)/2)+k2;))... (?)

[Dinozzo13]

Bonsoir à toutes et à tous, je remercie d'avance ceux qui m’aideront ! Voilà un exercice sur lequel je bloque. En fait je "sais" les réponses mais je ne sais pas comment les démontrer ou expliquer la façon dont je les trouve! Voici l'énoncé :

Le but de l'exercice est de résoudre l'équation (E) : cos 3x = 0
1.a) Démontrer que x est solution de (E) si et seulement si 3x= (;)/2)+k2;) et 3x= -(;)/2)+k2;) avec k en entier relatif.
Je sais que les seuls points se situant sur l'axe des sinus (et donc d'abscisse 0) se trouvent en /2 et -;)/2 et que quelque soit le nombre de tours ajouté on retombe sur le même point. Mais comment l'expliquer dans un "langage mathématique" ?

b) Écrire les solutions de l'équation (E).
Les solutions sont donc -(;)/2)+k2;) et (;)/2)+k2;))... (?)

Salut !

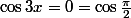
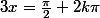
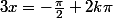
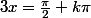
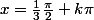équivaut donc à ou que l'on peut ramener à une seule solution ou encore avec .
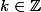
Après, résolve-t-on cette équation dans ou ?

[Loan]

Salut !

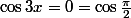
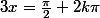
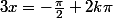
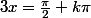
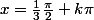équivaut donc à ou que l'on peut ramener à une seule solution ou encore avec .
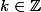
Après, résolve-t-on cette équation dans ou ?

Merci pour votre réponse, mais je ne comprend pas pourquoi vous enlevez le 2 de k2;)